题目内容
(14分)已知函数![]() ,设曲线
,设曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴的交点为
轴的交点为![]() ,其中
,其中![]() 为正实数
为正实数
(1)用![]() 表示
表示![]() ;
;
(2)![]() ,若
,若![]() ,试证明数列
,试证明数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
解析:(1)由题可得![]() ,所以在曲线上点
,所以在曲线上点![]() 处的切线方程为
处的切线方程为
![]() ,即
,即![]() -----------------2分
-----------------2分
令![]() ,得
,得![]() ,即
,即![]()
由题意得![]() ,所以
,所以![]() -----------------4分
-----------------4分
(2)因为![]() ,所以
,所以

即![]() ,所以数列
,所以数列![]() 为等比数列故
为等比数列故![]() ---8分
---8分
(3)当![]() 时,
时,![]()
当![]() 时,
时,![]()
所以数列![]() 的通项公式为
的通项公式为![]() ,故数列
,故数列![]() 的通项公式为
的通项公式为![]()
![]() ①
①
①![]() 的
的![]() ②
②
①![]() ②得
②得![]()

练习册系列答案
相关题目
 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示 ;
; ,若
,若 ,试证明数列
,试证明数列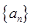 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 ,求
,求 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示 ;
; ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 ,求
,求