题目内容
7.已知函数f(x)=$\sqrt{x+1}$-$\sqrt{x}$,则f(x)有最大值为1.分析 先求出函数的定义域,利用分子有理化,判断函数的单调性即可.
解答 解:由$\left\{\begin{array}{l}{x+1≥0}\\{x≥0}\end{array}\right.$得$\left\{\begin{array}{l}{x≥-1}\\{x≥0}\end{array}\right.$,即x≥0,则函数的定义域为[0,+∞),
f(x)=$\sqrt{x+1}$-$\sqrt{x}$=$\frac{(\sqrt{x+1}-\sqrt{x})(\sqrt{x+1}+\sqrt{x})}{\sqrt{x+1}+\sqrt{x}}$=$\frac{1}{\sqrt{x}+\sqrt{x+1}}$,则f(x)为减函数,
则函数有最大值,此时最大值为f(0)=1,
故答案为:大,1
点评 本题主要考查函数最值的求解,利用分子有理化是解决本题的关键.

练习册系列答案
相关题目
18.f(x)=-2x2+mx-3在(-∞,3]上是增函数,则实数m的取值范围是( )
| A. | {1,2} | B. | [6,+∞) | C. | [12,+∞) | D. | (-∞,6] |
15.执行下面的程序框图,若p=0.95,则输出的n=( )
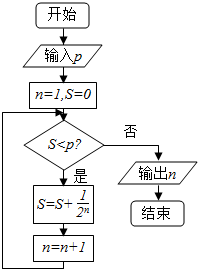

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
2.已知函数f(x)=$\frac{1}{x+1}$,则函数f(x)的定义域是( )
| A. | {x|x≠1} | B. | {x|x≠0} | C. | {x|x≠-1} | D. | x∈R |
19.数据5,7,7,8,10,11的方差是( )
| A. | 24 | B. | 10 | C. | 4 | D. | 2 |