题目内容
17.设x,y满足$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,求①μ=x2+y2,求最大值和最小值;②μ=$\frac{y}{x-5}$,求最大值和最小值.分析 作出不等式组对应的平面区域,利用目标函数的几何意义,进行求解即可.
解答 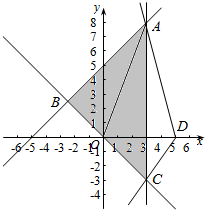 解:作出不等式组对应的平面区域,
解:作出不等式组对应的平面区域,
①μ=x2+y2的几何意义是区域内的点到原点的距离的平方,
由图象知μ=x2+y2的最小值为0,
OA的值最大,
由$\left\{\begin{array}{l}{x=3}\\{x-y+5=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=3}\\{y=8}\end{array}\right.$,即A(3,8),
此时μ=32+82=9+64=73;
②μ=$\frac{y}{x-5}$的几何意义是区域内的点到定点D(5,0)的斜率,
由图象知AD的斜率最小,此时k=$\frac{8}{3-5}=\frac{8}{-2}$=-4,
AD的斜率最大,由$\left\{\begin{array}{l}{x=3}\\{x+y=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=-3}\end{array}\right.$,即C(3,-3)
此时k=$\frac{-3}{3-5}=\frac{-3}{-2}$=$\frac{3}{2}$.
点评 本题主要考查线性规划的应用,利用两点间的距离公式以及直线的斜率公式是解决本题的关键.

练习册系列答案
相关题目
8.已知等比数列{an}中,8a2+a5=0,则$\frac{S_4}{S_2}$=( )
| A. | -2 | B. | 1 | C. | 2 | D. | 5 |
12.已知集合A={x|x2-1=0},则下列式子表示错误的是( )
| A. | 1∈A | B. | {1}∈A | C. | ∅⊆A | D. | {1,-1}⊆A |
9.在与水平地面垂直的墙壁上挂有一幅矩形画,画的上下边缘在观察着水平视线上方a m和b m处,要使观察者的视角最大,观察者与墙的距离为( )
| A. | $\sqrt{ab}m$ | B. | $\frac{a+b}{2}m$ | C. | am | D. | bm |
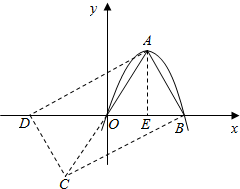 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.