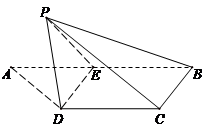题目内容
如图在直三棱柱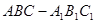 中,
中,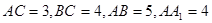 .
.
(Ⅰ)求证: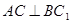 ;(Ⅱ)求二面角
;(Ⅱ)求二面角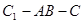 的余弦值大小;
的余弦值大小;
(Ⅲ)在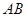 上是否存在点
上是否存在点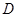 ,使得
,使得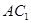 ∥平面
∥平面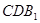 , 若存在,试给出证明;若不存在,请说明理由.
, 若存在,试给出证明;若不存在,请说明理由.
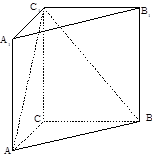
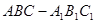 中,
中,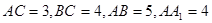 .
.(Ⅰ)求证:
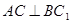 ;(Ⅱ)求二面角
;(Ⅱ)求二面角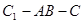 的余弦值大小;
的余弦值大小;(Ⅲ)在
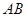 上是否存在点
上是否存在点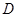 ,使得
,使得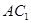 ∥平面
∥平面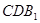 , 若存在,试给出证明;若不存在,请说明理由.
, 若存在,试给出证明;若不存在,请说明理由.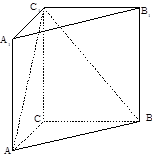
解法一(Ⅰ)在直三棱柱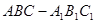 中,
中, 底面
底面 ,
,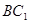 在底面上的射影为
在底面上的射影为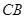 .
.
由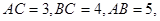 可得
可得 .
.
所以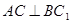 . (Ⅱ)过
. (Ⅱ)过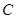 作
作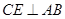 于
于 ,连结
,连结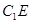 .
.
由 底面
底面 可得
可得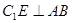 .故
.故 为二面角
为二面角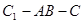 的平面角.
的平面角.
在 中,
中,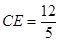 ,
,
在Rt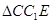 中,
中,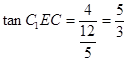 ,
,
故所求二面角的余弦值大小为.

(Ⅲ)存在点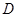 使
使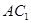 ∥平面
∥平面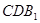 ,且
,且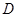 为
为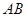 中点,下面给出证明.设
中点,下面给出证明.设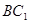 与
与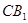 交于点
交于点 则
则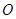 为
为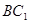 中点.
中点.
在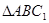 中, 连结
中, 连结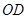 ,
,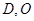 分别为
分别为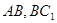 的中点,故
的中点,故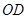 为
为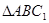 的中位线,
的中位线,
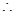
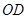 ∥
∥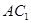 ,又
,又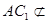 平面
平面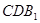 ,
,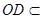 平面
平面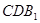 ,
, 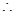
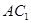 ∥平面
∥平面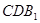 .
.
故存在点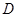 为
为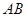 中点,使
中点,使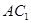 ∥平面
∥平面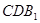 .
.
解法二 直三棱柱
直三棱柱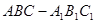 ,底面三边长
,底面三边长 ,
,
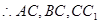 两两垂直.
两两垂直.
如图以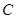 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系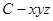 ,则
,则

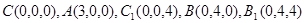 .
.
(Ⅰ)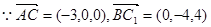 ,
,
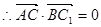 ,故
,故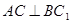 .
.
(Ⅱ)平面 的一个法向量为
的一个法向量为 ,
,
设平面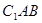 的一个法向量为
的一个法向量为 ,
,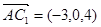 ,
,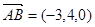 ,
,
由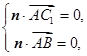 得
得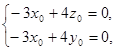
令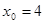 ,则
,则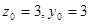 .则
.则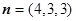 .故
.故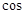 <
< >=
>=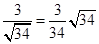 .
.
所求二面角的余弦值大小为.
(3)同上
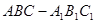 中,
中, 底面
底面 ,
,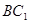 在底面上的射影为
在底面上的射影为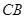 .
.由
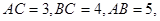 可得
可得 .
.所以
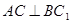 . (Ⅱ)过
. (Ⅱ)过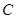 作
作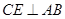 于
于 ,连结
,连结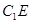 .
.由
 底面
底面 可得
可得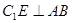 .故
.故 为二面角
为二面角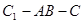 的平面角.
的平面角.在
 中,
中,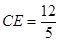 ,
,在Rt
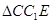 中,
中,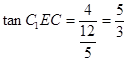 ,
,故所求二面角的余弦值大小为.


(Ⅲ)存在点
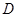 使
使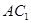 ∥平面
∥平面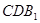 ,且
,且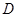 为
为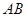 中点,下面给出证明.设
中点,下面给出证明.设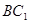 与
与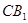 交于点
交于点 则
则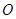 为
为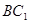 中点.
中点.在
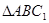 中, 连结
中, 连结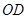 ,
,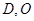 分别为
分别为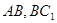 的中点,故
的中点,故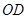 为
为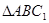 的中位线,
的中位线,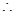
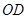 ∥
∥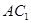 ,又
,又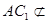 平面
平面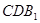 ,
,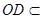 平面
平面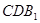 ,
, 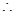
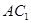 ∥平面
∥平面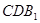 .
.故存在点
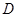 为
为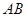 中点,使
中点,使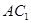 ∥平面
∥平面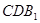 .
. 解法二
 直三棱柱
直三棱柱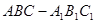 ,底面三边长
,底面三边长 ,
,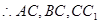 两两垂直.
两两垂直.如图以
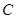 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系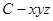 ,则
,则
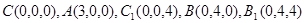 .
.(Ⅰ)
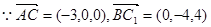 ,
,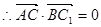 ,故
,故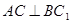 .
. (Ⅱ)平面
 的一个法向量为
的一个法向量为 ,
,设平面
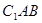 的一个法向量为
的一个法向量为 ,
,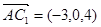 ,
,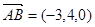 ,
,由
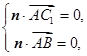 得
得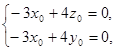
令
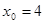 ,则
,则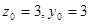 .则
.则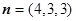 .故
.故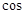 <
< >=
>=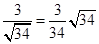 .
.所求二面角的余弦值大小为.

(3)同上
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
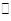 a,那么c与b的位置关系是( )
a,那么c与b的位置关系是( )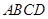 是矩形,
是矩形,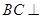 平面
平面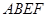 ,四边形
,四边形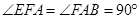 ,
,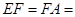
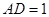 ,点
,点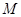 是
是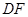 的中点,
的中点,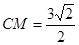 .
.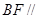 平面
平面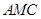 ;
;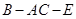 的余弦值.
的余弦值. 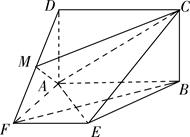
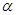 、
、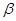 是空间不同的平面,a、b是空间不同的直线,下列命题错误的是( )
是空间不同的平面,a、b是空间不同的直线,下列命题错误的是( )

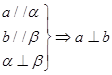
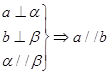
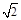 ,AB=1,E是DD1的中点。
,AB=1,E是DD1的中点。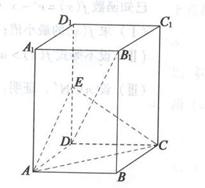
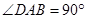 ,
,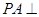 平面ABCD,PA=AB=BC=3,梯形上底AD=1。
平面ABCD,PA=AB=BC=3,梯形上底AD=1。 平面PAB;
平面PAB;
 中,已知
中,已知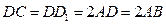 ,
,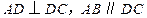 .
.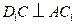 ;
;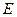 是
是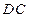 上一点,试确定
上一点,试确定 平面
平面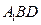 ,并证明.
,并证明.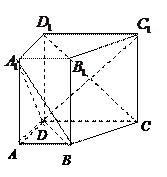
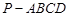 中,底面
中,底面 是直角梯形,
是直角梯形,
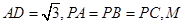 是线段
是线段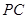 上不同于
上不同于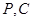 的任意一点,且
的任意一点,且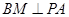

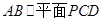 ;
;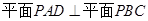 ;
;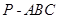 的体积。
的体积。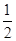 AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.
AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.