题目内容
线段AB过x轴正半轴上一定点M(m,0),两端点A、B到x轴的距离之积为2m,O为坐标原点,以x轴为对称轴,经过A、O、B三点作抛物线.
(1)求这条抛物线方程;
(2)若∠AOB=
,求m的最大值.
(1)求这条抛物线方程;
(2)若∠AOB=
| 3π | 4 |
分析:(1)设抛物线方程、直线AB的方程,联立这两个方程组消去x,利用两端点A、B到x轴的距离之积为2m,可求m的值,从而可得抛物线方程;
(2)利用tan(∠AOM+∠BOM)=-1,结合韦达定理,确定k、m的关系式,从而可得不等式,由此可求m的最大值.
(2)利用tan(∠AOM+∠BOM)=-1,结合韦达定理,确定k、m的关系式,从而可得不等式,由此可求m的最大值.
解答:解:(1)可设抛物线方程为y2=2px(p>0),
设直线AB的方程为y=k(x-m)(k≠0)…(2分)
联立这两个方程组消去x得,ky2-2py-2pkm=0,…(4分)
设A(x1,y1),B(x2,y2),由已知得|y1|•|y2|=2m,注意到y1•y2<0,所以y1•y2=-2m,
又y1•y2=-2pm,所以-2m=-2pm,因为m>0,所以p=1.
所以抛物线方程为y2=2x;…(6分)
(2)因为∠AOB=
,所以tan∠AOB=-1,即tan(∠AOM+∠BOM)=-1
又tan∠AOM=
=
,tan∠BOM=
=-
,
所以
=-1,
整理得y1y2+4=2(y1-y2).…(8分)
因为y1y2=-2m,所以y1-y2=2-m>0,从而(y1-y2)2=(2-m)2,
即(y1-y2)2-4y1y2=(2-m)2,所以(
)2+8m=(2-m)2,即
=m2-12m+4,
因此m2-12m+4>0,…(10分)
又当AB⊥x轴时,y1+y2=0,所以8m=(2-m)2,即m2-12m+4=0,
于是m2-12m+4≥0,且0<m<2,解之不等式组得到0<m≤6-4
.
故m的最大值是6-4
.…(12分)
设直线AB的方程为y=k(x-m)(k≠0)…(2分)
联立这两个方程组消去x得,ky2-2py-2pkm=0,…(4分)
设A(x1,y1),B(x2,y2),由已知得|y1|•|y2|=2m,注意到y1•y2<0,所以y1•y2=-2m,
又y1•y2=-2pm,所以-2m=-2pm,因为m>0,所以p=1.
所以抛物线方程为y2=2x;…(6分)
(2)因为∠AOB=
| 3π |
| 4 |
又tan∠AOM=
| y1 |
| x1 |
| 2 |
| y1, |
| -y2 |
| x2 |
| 2 |
| y2 |
所以
| ||||
1-
|
整理得y1y2+4=2(y1-y2).…(8分)
因为y1y2=-2m,所以y1-y2=2-m>0,从而(y1-y2)2=(2-m)2,
即(y1-y2)2-4y1y2=(2-m)2,所以(
| 2 |
| k |
| 4 |
| k2 |
因此m2-12m+4>0,…(10分)
又当AB⊥x轴时,y1+y2=0,所以8m=(2-m)2,即m2-12m+4=0,
于是m2-12m+4≥0,且0<m<2,解之不等式组得到0<m≤6-4
| 2 |
故m的最大值是6-4
| 2 |
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查解不等式,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
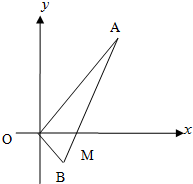 如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.
如图,线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线.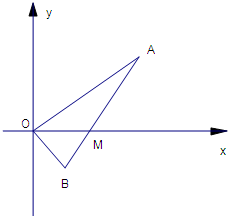 (理)线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴的距离之积为3m.以x轴为对称轴,过A、O、B作抛物线,
(理)线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴的距离之积为3m.以x轴为对称轴,过A、O、B作抛物线,
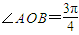 ,求m的最大值.
,求m的最大值.