Question

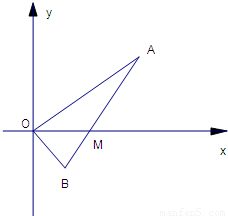
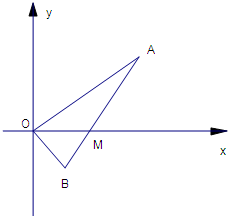（理）线段AB过x轴正半轴上一点M（m，0）（m＞0），端点A、B到x轴的距离之积为3m．以x轴为对称轴，过A、O、B作抛物线，
（1）求抛物线方程；
（2）若直线AB的斜率为

1

2

，求当0＜m＜3时，tan∠AOB的取值范围．

Answer 1

分析：（1）由于线段AB过x轴正半轴上一点M（m，0），可设方程为x-m=ty．假设抛物线方程为y²=2px（p＞0），联立消去x得y²-2pty-2pm=0，利用根与系数的关系及端点A、B到x轴的距离之积为3m，可求抛物线的方程．
（2）用A，B的坐标表示出tan∠AOB得到m的函数，再根据0＜m＜3，可确定tan∠AOB的取值范围．

解答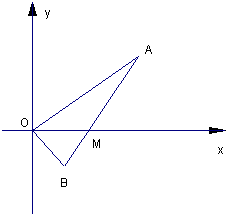：解：（1）设抛物线方程为y²=2px（p＞0），A（x₁，y₁），B（x₂，y₂），（y₁＞0，y₂＜0）．
由已知得y₁y₂=-3m．再设AB方程为：x-m=ty．
由

x-m=ty y2=2px

得y²-2pty-2pm=0∴y₁y₂=-3m=-2pm，∴2p=3，所求抛物线方程为y²=3x-------------------------6′
（2）由（1）A(

y12

3

，y1)（7），B(

y22

3

，y2)，t=2，y₁，y₂是方程y²-6y-3m=0（11）的两根，
所以y₁+y₂=6，∴y₁y₂=-3m，
tan∠AOB=

kOA-kOB

1+kOAkOB

=

3 y1 - 3 y2

1+ 3 y1 • 3 y2

=

3(y2-y1)

y1y2+9

=

-3 (y1+y2)2-4y1y2

y1y2+9

=

2 3 • 3+m

m-3

-------------10′
令s=m-3，则-3＜s＜0，设g(s)=

3+m

m-3

=

s+6

s

=-

6( 1 s + 1 12 )2- 1 24

，
又

1

s

＜-

1

3

∴g(s)＜

-1

3

，∴tan∠AOB＜-2----------------------------14′

点评：本题主要考查抛物线方程的求解，考查利用函数的思想解决取值范围问题，属于中档题．