题目内容
(13分)已知函数![]()
(1)当![]() 时,证明:函数
时,证明:函数![]() 只有一个零点;
只有一个零点;
(2)若函数![]() 在区间
在区间![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
解析:(Ⅰ)当a=1时,![]() ,其定义域是
,其定义域是![]() ,
,
![]() ………(1分)
………(1分)
令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() .
.
![]() ,
,![]() 舍去.
舍去.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴函数![]() 在区间(0,1)上单调递增,在区间
在区间(0,1)上单调递增,在区间![]() 上单调递减(4分)
上单调递减(4分)
∴当x=1时,函数![]() 取得最大值,其值为
取得最大值,其值为![]() .
.
当![]() 时,
时,![]() ,即
,即![]() .
.
∴函数![]() 只有一个零点. ………………(6分)
只有一个零点. ………………(6分)
(Ⅱ)法一:因为![]() 其定义域为
其定义域为![]() ,
,
所以![]() ……(7分)
……(7分)
①当a=0时,![]() 在区间
在区间![]() 上为增函数,不合题意(8分)
上为增函数,不合题意(8分)
②当a>0时,![]() 等价于
等价于![]() ,即
,即![]() .
.
此时![]() 的单调递减区间为
的单调递减区间为![]() .
.
依题意,得![]() 解之得
解之得![]() . …………………(10分)
. …………………(10分)
③当a<0时,![]() 等价于
等价于![]() ,即
,即![]() ?
?
此时![]() 的单调递减区间为
的单调递减区间为![]() ,
,
![]() 得
得![]()
综上,实数a的取值范围是![]() ………(13分)
………(13分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
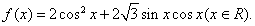
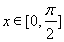
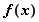

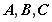
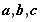
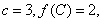
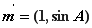
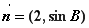
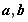

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
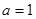 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.