题目内容

4．椭圆$\frac{{x}^{2}}{4}$+y2=1的左、右焦点分别为F1、F2，过F1的直线l交椭圆于A、B两点，则△ABF2的周长为（　　）
A．4B．8C．12D．16

分析 求得椭圆的a=2，再由椭圆的定义可得△AF1B的周长为c=4a=8．

解答 解：椭圆 $\frac{x^2}{16}$+$\frac{y^2}{9}$=1的a=4，
由椭圆的定义可得，
△AF2B的周长为c=|AB|+|AF2|+|BF2|
=（|AF2|+|AF1|）+（|BF1|+|BF2|）
=2a+2a=4a=8．
故选B．

点评 本题考查椭圆的定义、方程和性质，主要考查椭圆的定义的运用，考查运算能力，属于基础题．

练习册系列答案
相关题目
13．对于集合A、B，定义A+B={x+y|x∈A，y∈B}，下列命题：
①A+B=B+A；
②（A+B）+C=A+（B+C）；
③若A+A=B+B，则A=B；
④若A+C=B+C，则A=B．
其中正确的命题是（　　）
A．①B．①②C．②③D．①④
14．设平面α⊥平面β，直线a?α，直线b?β，且a⊥b，则（　　）
A．a⊥βB．b⊥α
C．a⊥β与b⊥α中至少有一个成立D．a⊥β与b⊥α同时成立
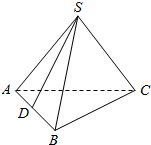11．如图，在正四面体S-ABC（四个面都是等边三角形）中，点D是棱AB的中点，则异面直线SD和BC所成角的余弦值是$\frac{\sqrt{3}}{6}$．
18．三棱锥P-ABC中，已知∠APC=∠BPC=∠APB=$\frac{π}{3}$，点M是△ABC的重心，且$\overrightarrow{PA}•\overrightarrow{PB}$+$\overrightarrow{PB}•\overrightarrow{PC}$+$\overrightarrow{PC}•\overrightarrow{PA}$=9．则|$\overrightarrow{PM}$|的最小值为2．
9．f（x）=ax3-x2+$\frac{1}{3}$x+1在（-∞，+∞）上恒为单调递增函数，则实数a的取值范围[1，+∞）．
16．如果数列{an}同时满足以下两个条件：（1）各项均不为0；（2）存在常数k，对任意n∈N*，an+12=anan+2+k都成立．则称这样的数列{an}为“k类等比数列”．
（Ⅰ）若数列{an}满足an=3n+1，证明数列{an}为“k类等比数列”，并求出相应的k；
（Ⅱ）若数列{an}为“3类等比数列”，且满足a1=1，a2=2，问是否存在常数l，使得an+an+2=lan+1对于任意n∈N*都成立？若存在，求出l；若不存在，请举出反例．
13．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为$\frac{\sqrt{2}}{2}$，点（$\sqrt{2}$，$\sqrt{3}$）在椭圆E上．
（1）求椭圆E的方程；
（2）设过点P（2，1）的直线l与椭圆相交于A、B两点，若AB的中点恰好为点P，求直线l的方程．
14．下列函数中，既是奇函数，又在定义域内为减函数的是（　　）
A．y=（${\frac{1}{2}}$）xB．y=-x2C．y=-x3D．y=log3（-x）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网