题目内容
9.f(x)=ax3-x2+$\frac{1}{3}$x+1在(-∞,+∞)上恒为单调递增函数,则实数a的取值范围[1,+∞).分析 已知函数f(x)=ax3-x2+$\frac{1}{3}$x+1在(-∞,+∞)上单调递增,对其进行求导转化成f′(x)≥0在x∈R恒成立,从而求解;
解答 解:∵函数f(x)=ax3-x2+$\frac{1}{3}$x+1在(-∞,+∞)上单调递增,
∴f′(x)=3ax2-2x+$\frac{1}{3}$≥0,在x∈R恒成立,
∴a>0,△=4-4×3a×$\frac{1}{3}$≤0,
∴a≥1,
故答案为:[1,+∞).
点评 此题主要考查函数的单调性与导数的关系,将问题转化为二次函数的恒成立,是一道中档题.

练习册系列答案
相关题目
19.设S是整数集Z的非空子集,如果?a,b∈Z,都有a2-b2∈S,则称S是一个好集,已知S是一个“好集”,下面命题为假命题的是( )
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |
16.在△ABC中,AB=2,BC=3,D是三角形内一点,CD=2,使∠B+∠ADC=180°,问求当∠B为何值时,△ABC和△ADC面积之差最大?(∠B=$\frac{π}{4}$时,面积之差最大)
14.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1、F2,若以F1F2为直径的圆与椭圆有交点,则椭圆离心率e的取值范围为( )
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{{\sqrt{2}}}{2}$,1) | C. | (0,$\frac{1}{2}$] | D. | (0,$\frac{{\sqrt{2}}}{2}}$] |
 如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.
如图,已知△ABC,A(7,8),B(3,5),C(4,3),M,N,D分别是AB,AC,BC的中点,且MN与AD交于F.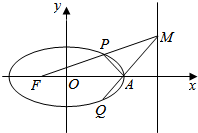 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左焦点为F(-1,0),M为右准线x=4上的一动点(不在x轴上),线段FM交椭圆于点P,MA与椭圆的另一交点为Q.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)左焦点为F(-1,0),M为右准线x=4上的一动点(不在x轴上),线段FM交椭圆于点P,MA与椭圆的另一交点为Q.