题目内容
 四棱锥P-ABCD的底面ABCD为正方形,且PD垂直于底面ABCD,
四棱锥P-ABCD的底面ABCD为正方形,且PD垂直于底面ABCD,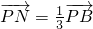 ,则三棱锥P-ANC与四棱锥P-ABCD的体积比为
,则三棱锥P-ANC与四棱锥P-ABCD的体积比为
- A.1:2
- B.1:3
- C.1:6
- D.1:8
C
分析:由于利用提及的分割原理可知四棱锥P-ABCD的体积为VP-ABCD=2VB-PAC,又由于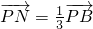 ,所以点N为PB的三等分点,所以利用利用体积公式及成比列可知VP-ABCD=6VN-PAC.
,所以点N为PB的三等分点,所以利用利用体积公式及成比列可知VP-ABCD=6VN-PAC.
解答:因为四棱锥P-ABCD的体积为:VP-ABCD=VB-PAC+VD-PAC而VB-PAC=VD-PAC,所以VP-ABCD=2VB-PAC,又由于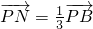 ,所以利用三棱锥的体积公式及三棱锥的体积具有定点可以轮换的原理可知:VB-PAC=3VN-PAC,所以VP-ABCD=6VN-PAC.所以
,所以利用三棱锥的体积公式及三棱锥的体积具有定点可以轮换的原理可知:VB-PAC=3VN-PAC,所以VP-ABCD=6VN-PAC.所以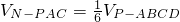 .
.
故选C
点评:此题考查了体积公式及成比列的性质,还考查了体积的分割原理,及三棱锥的体积定点可以进行轮换法.
分析:由于利用提及的分割原理可知四棱锥P-ABCD的体积为VP-ABCD=2VB-PAC,又由于
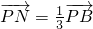 ,所以点N为PB的三等分点,所以利用利用体积公式及成比列可知VP-ABCD=6VN-PAC.
,所以点N为PB的三等分点,所以利用利用体积公式及成比列可知VP-ABCD=6VN-PAC.解答:因为四棱锥P-ABCD的体积为:VP-ABCD=VB-PAC+VD-PAC而VB-PAC=VD-PAC,所以VP-ABCD=2VB-PAC,又由于
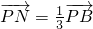 ,所以利用三棱锥的体积公式及三棱锥的体积具有定点可以轮换的原理可知:VB-PAC=3VN-PAC,所以VP-ABCD=6VN-PAC.所以
,所以利用三棱锥的体积公式及三棱锥的体积具有定点可以轮换的原理可知:VB-PAC=3VN-PAC,所以VP-ABCD=6VN-PAC.所以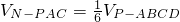 .
.故选C
点评:此题考查了体积公式及成比列的性质,还考查了体积的分割原理,及三棱锥的体积定点可以进行轮换法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
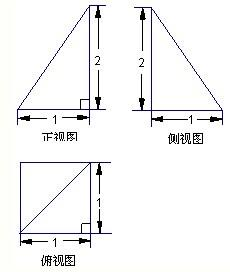 已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )
已知四棱锥P-ABCD的三视图如图所示,则这个四棱锥的体积为( )A、
| ||
| B、1 | ||
C、
| ||
D、
|
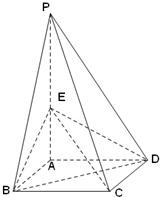 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点. 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE= 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: