题目内容
设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=x0,则称x0是f(x)的一个不动点,也称f(x)在区间D上有不动点.
(1)证明f(x)=2x-2x-3在区间(1,4)上有不动点;
(2)若函数f(x)=ax2-x-a+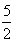 在区间[1,4]上有不动点,求常数a的取值范围.
在区间[1,4]上有不动点,求常数a的取值范围.
(1)证明f(x)=2x-2x-3在区间(1,4)上有不动点;
(2)若函数f(x)=ax2-x-a+
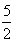 在区间[1,4]上有不动点,求常数a的取值范围.
在区间[1,4]上有不动点,求常数a的取值范围. 解:(1)依题意,“f(x)在区间D上有不动点”当且仅当“F(x)= f(x)-x在区间D上有零点”,
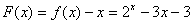 在区间[1,4]上是一条连续不断的曲线,
在区间[1,4]上是一条连续不断的曲线,
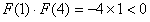 ,
,
所以,函数F(x)= f(x)-x在区间(1,4)内有零点,
即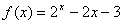 在区间(1,4)上有不动点。
在区间(1,4)上有不动点。
(2)依题意,存在x∈[1,4],使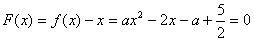 ,
,
当x=1时,使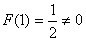 ;
;
当x≠1时,解得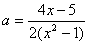 ,
,
由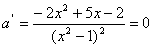 ,得x=2或
,得x=2或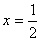 (
(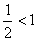 ,舍去),
,舍去),
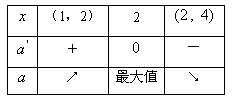 ,
,
所以,当x=2时,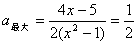 ,
,
所以,常数a的取值范围是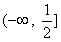 。
。
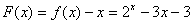 在区间[1,4]上是一条连续不断的曲线,
在区间[1,4]上是一条连续不断的曲线,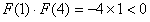 ,
,所以,函数F(x)= f(x)-x在区间(1,4)内有零点,
即
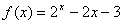 在区间(1,4)上有不动点。
在区间(1,4)上有不动点。(2)依题意,存在x∈[1,4],使
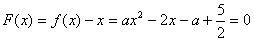 ,
,当x=1时,使
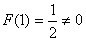 ;
;当x≠1时,解得
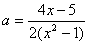 ,
,由
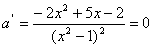 ,得x=2或
,得x=2或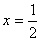 (
(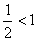 ,舍去),
,舍去), ,
,所以,当x=2时,
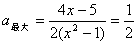 ,
,所以,常数a的取值范围是
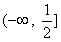 。
。
练习册系列答案
相关题目
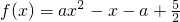 在区间[1,4]上有不动点,求常数a的取值范围.
在区间[1,4]上有不动点,求常数a的取值范围. 在区间[1,4]上存在次不动点,则实数a的取值范围是 .
在区间[1,4]上存在次不动点,则实数a的取值范围是 .