题目内容
设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=-x0,则称x0是f(X)的一个“次不动点”,也称f(x)在区间D上存在次不动点.若函数f(x)=ax2-3x-a+
在区间[1,4]上存在次不动点,则实数a的取值范围是
| 5 |
| 2 |
(-∞,
]
| 1 |
| 2 |
(-∞,
]
.| 1 |
| 2 |
分析:根据“f(x)在区间D上有次不动点”当且仅当“F(x)=f(x)+x在区间D上有零点”,依题意,存在x∈[1,4],使F(x)=f(x)+x=ax2-2x-a+
=0,讨论将a分离出来,利用导数研究出等式另一侧函数的取值范围即可求出a的范围.
| 5 |
| 2 |
解答:解:依题意,存在x∈[1,4],使F(x)=f(x)+x=ax2-2x-a+
=0,
当x=1时,使F(1)=
≠0(6分);
当x≠1时,解得a=
(8分),
由a′=
=0(9分),
得x=2或x=
(
<1,舍去)(10分),
(12分),当x=2时,a最大=
=
(13分),
所以常数a的取值范围是(-∞,
](14分).
故答案为:(-∞,
].
| 5 |
| 2 |
当x=1时,使F(1)=
| 1 |
| 2 |
当x≠1时,解得a=
| 4x-5 |
| 2(x2-1) |
由a′=
| -2x2+5x-2 |
| (x2-1)2 |
得x=2或x=
| 1 |
| 2 |
| 1 |
| 2 |
| x | (1,2) | 2 | (2,4) |
| a′ | + | 0 | - |
| a | ↗ | 最大值 | ↘ |
| 4x-5 |
| 2(x2-1) |
| 1 |
| 2 |
所以常数a的取值范围是(-∞,
| 1 |
| 2 |
故答案为:(-∞,
| 1 |
| 2 |
点评:本题主要考查了函数与方程的综合运用,以及函数零点和利用导数研究最值等有关知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
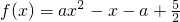 在区间[1,4]上有不动点,求常数a的取值范围.
在区间[1,4]上有不动点,求常数a的取值范围. 在区间[1,4]上存在次不动点,则实数a的取值范围是 .
在区间[1,4]上存在次不动点,则实数a的取值范围是 . 在区间[1,4]上有不动点,求常数a的取值范围.
在区间[1,4]上有不动点,求常数a的取值范围.