题目内容
已知 是复数,
是复数,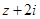 、
、 均为实数(
均为实数( 为虚数单位),且复数
为虚数单位),且复数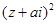 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围.
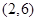 .
.
解析试题分析:设复数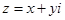 ,然后根据
,然后根据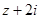 ,
, 为实数,建立关于
为实数,建立关于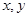 的方程,求出
的方程,求出 ,然后利用复数
,然后利用复数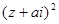 在复平面上对应的点在第一象限,可建立关于
在复平面上对应的点在第一象限,可建立关于 的不等式,求出
的不等式,求出 的取值范围.
的取值范围.
试题解析:设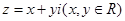
∴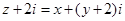 ,由题意得
,由题意得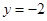
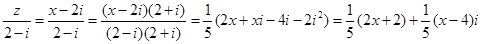
由题意得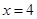 ,∴
,∴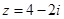
∵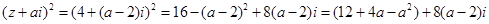
根据条件,可知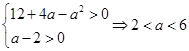
∴实数 的取值范围是
的取值范围是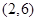 .
.
考点:1.复数的四则运算;2.复数的几何意义.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
题目内容
已知 是复数,
是复数,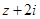 、
、 均为实数(
均为实数( 为虚数单位),且复数
为虚数单位),且复数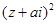 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围.
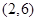 .
.
解析试题分析:设复数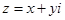 ,然后根据
,然后根据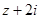 ,
, 为实数,建立关于
为实数,建立关于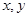 的方程,求出
的方程,求出 ,然后利用复数
,然后利用复数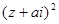 在复平面上对应的点在第一象限,可建立关于
在复平面上对应的点在第一象限,可建立关于 的不等式,求出
的不等式,求出 的取值范围.
的取值范围.
试题解析:设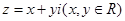
∴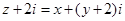 ,由题意得
,由题意得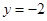
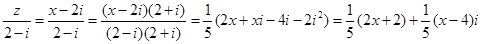
由题意得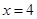 ,∴
,∴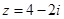
∵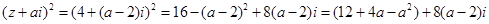
根据条件,可知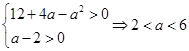
∴实数 的取值范围是
的取值范围是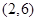 .
.
考点:1.复数的四则运算;2.复数的几何意义.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案