题目内容
(本小题满分10分)选修4-4:极坐标系与参数方程
在直角坐标系 中,曲线
中,曲线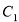 的参数方程为
的参数方程为 ,(
,(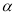 为参数),以原点
为参数),以原点 为极点,
为极点,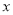 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线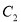 的极坐标方程为
的极坐标方程为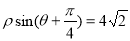 .
.
(1)求曲线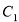 的普通方程与曲线
的普通方程与曲线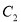 的直角坐标方程;
的直角坐标方程;
(2)设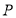 为曲线
为曲线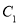 上的动点,求点
上的动点,求点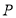 到
到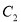 上点的距离的最小值.
上点的距离的最小值.
(1) ,
, ;(2)
;(2)
【解析】
试题分析:(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若 有范围限制,要标出
有范围限制,要标出 的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式
的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式 及
及 直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如
直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如 ,
, ,
, 的形式,进行整体代换,其中方程的两边同乘以(或同除以)
的形式,进行整体代换,其中方程的两边同乘以(或同除以) 及方程的两边平方是常用的变形方法.
及方程的两边平方是常用的变形方法.
试题解析:(1)由曲线 :
: 得
得
即:曲线 的普通方程为:
的普通方程为:
由曲线 :
: 得:
得:
即:曲线 的直角坐标方程为:
的直角坐标方程为: 5分
5分
(2) 由(1)知椭圆 与直线
与直线 无公共点,
无公共点,
椭圆上的点 到直线
到直线 的距离为
的距离为

所以当 时,
时, 的最小值为
的最小值为 10分
10分
考点:1、参数方程与普通方程的互化;2、点到直线的距离公式.
考点分析: 考点1:坐标系与参数方程 考点2:参数方程 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 中 “
中 “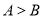 ”是“
”是“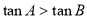 ”的( )
”的( ) 的焦点与双曲线
的焦点与双曲线 的右焦点重合,则该抛物线的准线方程为( )
的右焦点重合,则该抛物线的准线方程为( ) B.
B. C.
C. D.
D.
 中,含
中,含 项的系数为 .
项的系数为 .
 ,
, ,命题
,命题
 ,
, ,则( )
,则( ) 是假命题 B.命题
是假命题 B.命题 是真命题
是真命题 是真命题 D.命题
是真命题 D.命题 是假命题
是假命题  中,底面
中,底面 是等腰梯形,
是等腰梯形,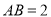 ,
,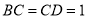
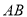 ∥
∥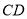 ,顶点
,顶点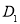 在底面
在底面 .
.
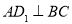 ;
;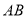 上是否存在点
上是否存在点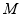 ,使得
,使得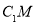 ∥平面
∥平面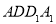 ?若存在,确定点
?若存在,确定点 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,右顶点为
,右顶点为 ,上顶点为
,上顶点为 ,若椭圆
,若椭圆 的距离为
的距离为 ,则椭圆
,则椭圆
 B.
B. C.
C. D.
D.
 中,底面
中,底面 是等腰梯形,
是等腰梯形, ∥
∥ ,
, ,
, ,顶点
,顶点 在底面
在底面 .
.
 ;
; 与直线
与直线 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的
所成角(锐角)的 ,集合
,集合 , 则
, 则 ( )
( ) B.
B. C.
C. D.
D.