题目内容
已知函数f(x),对任意x,y∈R,恒有f(x+y)=f(x)+f(y)成立,且当x>0时,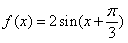 ,
,
(1)证明:f(x)是奇函数;
(2)求f(x)在R上的解析式。
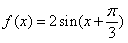 ,
,(1)证明:f(x)是奇函数;
(2)求f(x)在R上的解析式。
(1)证明:因为函数f(x),对任意x,y∈R,恒有f(x+y)=f(x)+ f(y)成立,所以f(0)=0,
令 ,
,
则f(-x)=-f(x),所以f(x)为奇函数。
(2)解:当x>0时, ;
;
当x>0时,-x<0, ,
,
由f(-x)=-f(x),得 ,
,
所以, 。
。
令
 ,
, 则f(-x)=-f(x),所以f(x)为奇函数。
(2)解:当x>0时,
 ;
;当x>0时,-x<0,
 ,
,由f(-x)=-f(x),得
 ,
, 所以,
 。
。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 满足对任意x1≠x2,都有
满足对任意x1≠x2,都有 满足对任意x1≠x2都有
满足对任意x1≠x2都有