题目内容
函数y=
-
(x∈(0,
))的值域是( )
| sin3x |
| sinx |
| cos5x |
| cosx |
| π |
| 2 |
分析:利用二倍角公式化简函数的解析式为y=-16(sin 2x-
)2+3,根据0<sinx<1,再利用二次函数的性质可得函数y的值域.
| 1 |
| 4 |
解答:解:∵函数y=
-
=
-
=3-4sin2x-
=3-4sin2x-4cos2x cos2x+3cos2x+2sin3xsinx
=3-4sin2x-4(1-sin2x)(1-2sin2x)+3(1-2sin2x)+2(3sinx-4sin3x)sinx
=2+8sin2x-16sin4x=-16(sin 2x-
)2+3,且 0<x<
,∴0<sinx<1,
∴当sin2x=
时,函数取得最大值为 3,当sinx 趋于1 时,函数的最小值趋于-6,
即函数的值域为 (-6,3],
故选 C.
| sin3x |
| sinx |
| cos5x |
| cosx |
| 3sinx-4sin3x |
| sinx |
| cos3xcos2x-sin3xsin2x |
| cosx |
=3-4sin2x-
| (4cos3x-3cosx)cos2x-sin3x• 2sinxcosx |
| cosx |
=3-4sin2x-4cos2x cos2x+3cos2x+2sin3xsinx
=3-4sin2x-4(1-sin2x)(1-2sin2x)+3(1-2sin2x)+2(3sinx-4sin3x)sinx
=2+8sin2x-16sin4x=-16(sin 2x-
| 1 |
| 4 |
| π |
| 2 |
∴当sin2x=
| 1 |
| 4 |
即函数的值域为 (-6,3],
故选 C.
点评:本题主要考查二倍角公式、正弦函数的定义域和值域,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
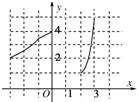 13、函数y=f(x)的图象如图所示.那么,f(x)的定义域是
13、函数y=f(x)的图象如图所示.那么,f(x)的定义域是