题目内容
设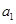 、
、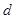 为实数,首项为
为实数,首项为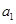 ,公差为
,公差为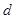 的等差数列
的等差数列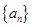 的前
的前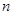 项和为
项和为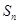 ,满足
,满足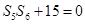 ,
,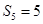 .
.
(1)求通项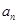 及
及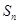 ;
;
(2)设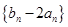 是首项为
是首项为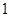 ,公比为
,公比为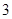 的等比数列,求数列
的等比数列,求数列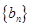 的通项公式及其前
的通项公式及其前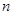 项和
项和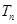 .
.
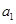 、
、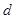 为实数,首项为
为实数,首项为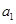 ,公差为
,公差为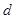 的等差数列
的等差数列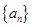 的前
的前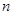 项和为
项和为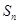 ,满足
,满足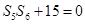 ,
,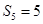 .
.(1)求通项
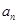 及
及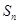 ;
;(2)设
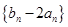 是首项为
是首项为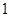 ,公比为
,公比为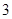 的等比数列,求数列
的等比数列,求数列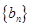 的通项公式及其前
的通项公式及其前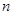 项和
项和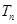 .
.(1) ,
, ;(2)
;(2) ,
, .
.
 ,
, ;(2)
;(2) ,
, .
.试题分析:(1)先求出
 求出来,然后将问题中的量利用
求出来,然后将问题中的量利用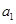 和
和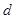 构造二元一次方程组,求出
构造二元一次方程组,求出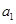 和
和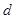 的值,进而确定
的值,进而确定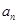 及
及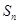 ;(2)先根据题中的已知条件求出
;(2)先根据题中的已知条件求出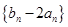 的通项公式,然后在(1)的基础上求出数列
的通项公式,然后在(1)的基础上求出数列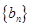 的通项公式,并根据数列
的通项公式,并根据数列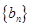 的通项结构选择分组求和法求出数列
的通项结构选择分组求和法求出数列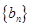 的前
的前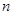 项和
项和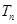 .
.试题解析:(1)
 ,
,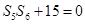 ,即
,即 ,
,于是有

 ,化简得
,化简得 ,解得
,解得 ,
, ,
, ;
;(2)由题意知
 ,
, .
.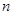 项和;2.分组求和法
项和;2.分组求和法
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 的通项
的通项 ,
, 满足关系
满足关系 ,且数列
,且数列 项和
项和
 .
. .
. 的前
的前 项和为
项和为 ,且
,且 .
. 满足
满足 ,求数列
,求数列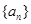 的首项
的首项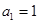 ,公差
,公差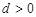 .且
.且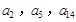 分别是等比数列
分别是等比数列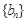 的
的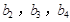 .
. 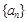 与
与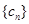 对任意自然数
对任意自然数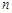 均有
均有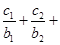 …
…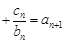 成立,求
成立,求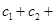 …
…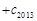 的值.
的值.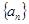 是公比为
是公比为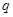 的等比数列,且
的等比数列,且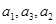 成等差数列.
成等差数列.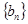 是以2为首项,
是以2为首项,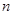 项和为
项和为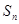 ,当n≥2时,比较
,当n≥2时,比较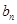 的大小,并说明理由.
的大小,并说明理由. 的前
的前 项和为
项和为 ,且
,且 ,则
,则 取最小值时,
取最小值时, 的值是( )
的值是( ) 中,
中, ,则前13项之和等于( )
,则前13项之和等于( )



 是等差数列
是等差数列 {
{ }的前n项和,
}的前n项和, ,
, ,
, (n>6),则n等于 ( )
(n>6),则n等于 ( )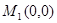 ,
,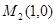 .以
.以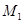 为圆心,
为圆心,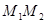 为半径作圆交
为半径作圆交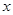 轴于点
轴于点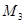 (异于
(异于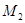 ),记作⊙
),记作⊙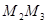 为半径作圆交
为半径作圆交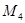 (异于
(异于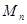 为圆心,
为圆心,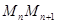 为半径作圆交
为半径作圆交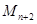 (异于
(异于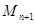 ),记作⊙
),记作⊙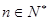 时,过原点作倾斜角为
时,过原点作倾斜角为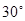 的直线与⊙
的直线与⊙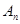 ,
,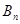 .考察下列论断:
.考察下列论断: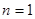 时,
时,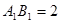 ;当
;当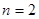 时,
时,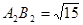 ;当
;当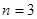 时,
时,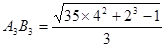 ;当
;当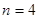 时,
时,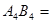 .
.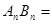 .
.