题目内容
已知椭圆的长轴长为2a,焦点是F1(-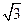 ,0)、F2(
,0)、F2(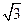 ,0),点F1到直线x=-
,0),点F1到直线x=-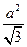 的距离为
的距离为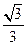 ,过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点,使得|F2B|=3|F2A|.
,过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点,使得|F2B|=3|F2A|.
(1)求椭圆的方程;
(2)求直线l的方程.
(1)∵F1到直线x=-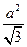 的距离为
的距离为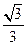 ,
,
∴-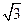 +
+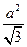 =
=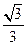 .
.
∴a2=4.
而c=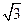 ,
,
∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,
∴所求椭圆的方程为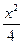 +y2=1.
+y2=1.
(2)设A(x1,y1)、B(x2,y2).
∵|F2B|=3|F2A|, ∴
∴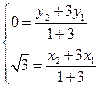
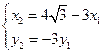
∵A、B在椭圆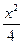 +y2=1上,
+y2=1上,
∴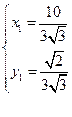 ∴l的斜
∴l的斜 率为
率为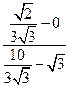 =
=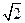 .
.
∴l的方程为y=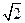 (x-
(x-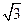 ),即
),即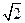 x-y-
x-y-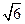 =0.
=0.
解析

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
在极坐标系中与圆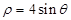 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A.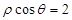 | B.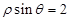 | C.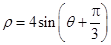 | D.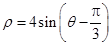 |
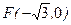 ,且过
,且过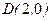 ,设点
,设点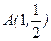 .
.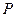 是椭圆上的动点,求线段
是椭圆上的动点,求线段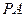 中点
中点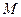 的轨迹方程;
的轨迹方程; ,记点P的轨迹为E.
,记点P的轨迹为E.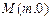 ,使
,使 恒成立,求实数m的值.
恒成立,求实数m的值. 相交于A、B两点。
相交于A、B两点。 ,焦距为2,求椭圆的标准方程;
,焦距为2,求椭圆的标准方程; (其中O为坐标原点),当椭圆的离率
(其中O为坐标原点),当椭圆的离率 时,求椭圆的长轴长的最大值。
时,求椭圆的长轴长的最大值。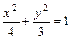 ,在曲线C上是否存在不同两点A、B关于直线
,在曲线C上是否存在不同两点A、B关于直线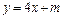 (m为常数)对称?若存在,求出
(m为常数)对称?若存在,求出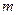 满足的条件;若不存在,说明理由。
满足的条件;若不存在,说明理由。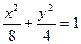 的左右焦点为
的左右焦点为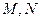 ;直线
;直线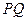 经过
经过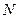 交椭圆于
交椭圆于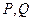 两点.
两点.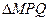 的周长为定值.
的周长为定值.
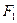 、
、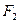 分别是椭圆
分别是椭圆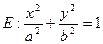 ,
,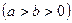
 的左、右焦点,
的左、右焦点,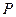 是该椭圆上一个动点,且
是该椭圆上一个动点,且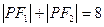 ,
,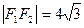 。
。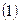 、求椭圆
、求椭圆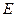 的方程;
的方程;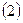 、求出以点
、求出以点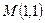 为中点的弦所在的直线方程。
为中点的弦所在的直线方程。