题目内容
在极坐标系中与圆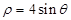 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A.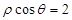 | B. | C. | D.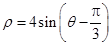 |
A
解析试题分析:由极坐标系下的方程与平面直角坐标系下的转化可知,圆的方程为 ,那么A中
,那么A中 是与圆相切的一条直线.
是与圆相切的一条直线.
考点:1.极坐标;2.直线与圆的位置关系.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
极坐标方程 表示的图形是( )
表示的图形是( )
| A.两个圆 | B.一个圆和一条直线 | C.一个圆和一条射线 | D.一条直线和一条射线 |
点 ,则它的极坐标是.( )
,则它的极坐标是.( )
A. | B. | C. | D. |
下列极坐标方程表示圆的是( )
A. | B. |
C. | D. |
直线 ,圆
,圆 ,直线
,直线 与圆C的位置关系是 ( )
与圆C的位置关系是 ( )
| A.相交 | B.相切 | C.相离 | D.不确定 |
在平面直角坐标系中,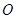 为原点,
为原点,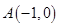 ,
,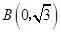 ,
,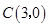 ,动点
,动点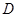 满足
满足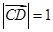 ,
,
则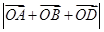 的取值范围是( )
的取值范围是( )
A.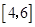 | B.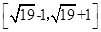 |
C.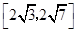 | D.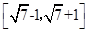 |
在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )
A.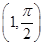 | B.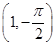 | C.(1,0) | D.(1,π) |
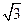 ,0)、F2(
,0)、F2(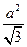 的距离为
的距离为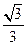 ,过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点,使得|F2B|=3|F2A|.
,过点F2且倾斜角为锐角的直线l与椭圆交于A、B两点,使得|F2B|=3|F2A|.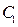 的方程为
的方程为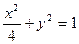 ,双曲线
,双曲线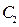 的左、右焦
的左、右焦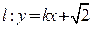 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。