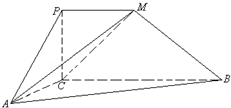
题目内容
平行四边形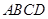 中,
中,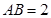 ,
,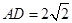 ,
,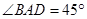 ,以
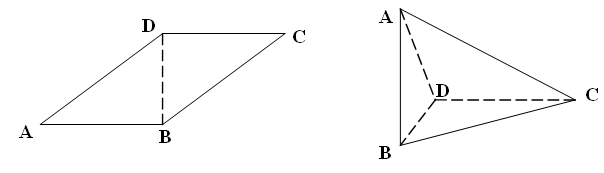
,以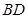 为折线,把
为折线,把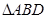 折起,使平面
折起,使平面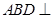 平面
平面 ,连结
,连结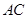 .
.
(Ⅰ)求证: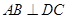 ;
;
(Ⅱ)求二面角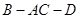 的大小.
的大小.
(Ⅰ)详见解析;(Ⅱ)二面角B AC D的大小是 .
.
解析试题分析:(Ⅰ)这是一个折叠问题,做这一类题需比较折叠前的图形,与折叠后的图形,观察那些元素位置关系没发生变化,那些边角关系发生变化,本题证明: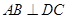 ,证明两线垂直,只需证明一线垂直另一线所在的平面,有原图易证
,证明两线垂直,只需证明一线垂直另一线所在的平面,有原图易证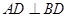 ,且平面
,且平面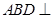 平面
平面 ,有面面垂直的性质可得
,有面面垂直的性质可得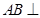 面
面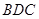 ,从而可得
,从而可得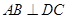 ;(Ⅱ)求二面角
;(Ⅱ)求二面角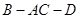 的大小,可用向量法求,需建立空间坐标,注意到
的大小,可用向量法求,需建立空间坐标,注意到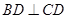 ,且平面
,且平面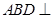 平面
平面 ,可以D为坐标原点,DB为
,可以D为坐标原点,DB为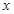 轴,DC为
轴,DC为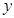 轴,过D垂直于平面BDC的射线为
轴,过D垂直于平面BDC的射线为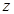 轴,建立空间直角坐标系,分别设平面ABC与平面DAC的法向量,分别计算出它们的法向量,利用法向量来求出二面角B AC D的大小.
轴,建立空间直角坐标系,分别设平面ABC与平面DAC的法向量,分别计算出它们的法向量,利用法向量来求出二面角B AC D的大小.
试题解析:(Ⅰ)在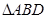 中,
中,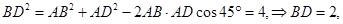 3分
3分
易得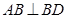 , 4分
, 4分 面
面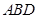
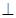 面
面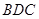
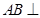 面
面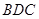
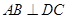 6分
6分
(Ⅱ)在四面体ABCD中,以D为原点,DB为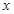 轴,DC为
轴,DC为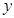 轴,过D垂直于平面BDC的射线为
轴,过D垂直于平面BDC的射线为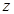 轴,建立如图空间直角坐标系.
轴,建立如图空间直角坐标系.
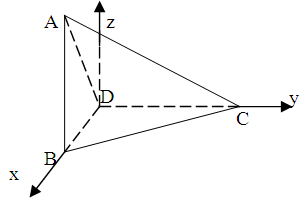
则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)
设平面ABC的法向量为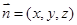 ,而
,而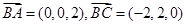 ,
,
由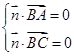 得:
得: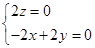 ,取
,取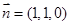 . 8分
. 8分
再设平面DAC的法向量为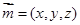 ,而
,而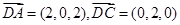 ,
,
由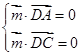 得:
得: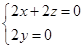 ,取
,取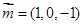 , 10分
, 10分
所以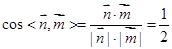 ,所以二面角B AC D的大小是
,所以二面角B AC D的大小是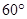 12分
12分
考点:线面垂直的判断,二面角的求法.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
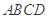 为正方形,
为正方形,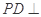 平面
平面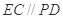 ,且
,且
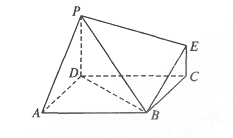
 平面
平面 ;
; 的体积;
的体积;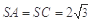 ,
,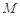 、
、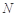 分别为
分别为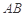 、
、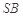 的中点.
的中点.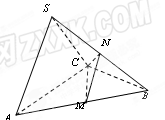
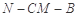 的余弦值;
的余弦值;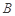 到平面
到平面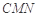 的距离.
的距离.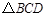 是等边三角形,
是等边三角形,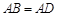 ,
,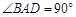 ,将
,将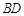 折叠到
折叠到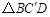 的位置,使得
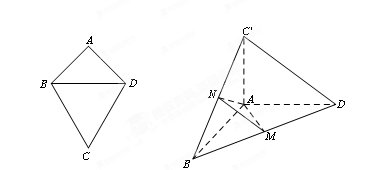
的位置,使得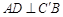 .
.
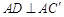 ;
;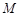 ,
,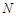 分别是
分别是 的中点,求二面角
的中点,求二面角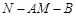 的余弦值.
的余弦值.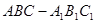 中,
中,
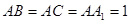 ,点
,点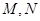 分别为
分别为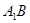 和
和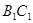 的中点.
的中点.
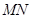 ∥平面
∥平面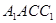 ;
;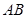 与
与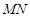 所成角的大小.
所成角的大小. 中,
中,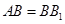 ,
,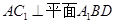 ,
,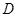 为的
为的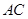 中点.
中点.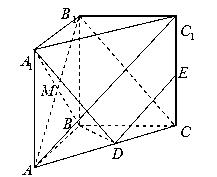
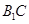 ∥平面
∥平面 ;
;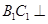 平面
平面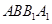 ;
;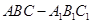 中,D、E分别为
中,D、E分别为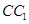 、AD的中点,F为
、AD的中点,F为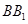 上的点,且
上的点,且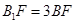
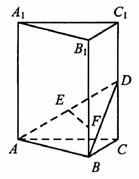
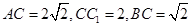 ,
,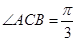 ,求二面角
,求二面角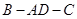 的大小.
的大小.