题目内容
已知椭圆 的一个焦点到长轴的两个端点的距离分别为
的一个焦点到长轴的两个端点的距离分别为 和
和 ,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E,F两点.
,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E,F两点.(1)求此椭圆的方程;
(2)若
 ,求k的值;
,求k的值;(3)求四边形AEBF面积的最大值.

【答案】分析:(1)由题意得 =1.(2)直线AB,EF的方程分别为x+2y=2,y=kx(k>0).设D(x,kx),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1=
=1.(2)直线AB,EF的方程分别为x+2y=2,y=kx(k>0).设D(x,kx),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1= .由此能求出k的值.
.由此能求出k的值.
(3)根据点到直线的距离公式,知点E,F到AB的距离,分别求出为h1,h2,|AB|= =
= ,由此能求出四边形AEBF的面积的最大值.
,由此能求出四边形AEBF的面积的最大值.
解答:解:(1)由题意 =1.
=1.
(2)直线AB,EF的方程分别为x+2y=2,y=kx(k>0).
设D(x,kx),E(x1,kx1),F(x2,kx2),其中x1<x2,
且x1,x2满足方程(1+4k2)x2=4,
故x2=-x1= .
.
由 ;
;
由D在AB上知x+2kx=2,
得x= .
.
所以 .
.
(3)根据点到直线的距离公式知,
点E,F到AB的距离分别为
h1= ,
,
又|AB|= =
= ,
,
所以四边形AEBF的面积为
S=
 .
.
当2k=1,即当k=
 .
.
点评:本题考查直线和椭圆的综合应用,解题时要认真审题,注意挖掘题中的隐含条件,合理地进行等价转化.
 =1.(2)直线AB,EF的方程分别为x+2y=2,y=kx(k>0).设D(x,kx),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1=
=1.(2)直线AB,EF的方程分别为x+2y=2,y=kx(k>0).设D(x,kx),E(x1,kx1),F(x2,kx2),其中x1<x2,且x1,x2满足方程(1+4k2)x2=4,故x2=-x1= .由此能求出k的值.
.由此能求出k的值.(3)根据点到直线的距离公式,知点E,F到AB的距离,分别求出为h1,h2,|AB|=
 =
= ,由此能求出四边形AEBF的面积的最大值.
,由此能求出四边形AEBF的面积的最大值.解答:解:(1)由题意
 =1.
=1.(2)直线AB,EF的方程分别为x+2y=2,y=kx(k>0).
设D(x,kx),E(x1,kx1),F(x2,kx2),其中x1<x2,
且x1,x2满足方程(1+4k2)x2=4,
故x2=-x1=
 .
.由
 ;
;由D在AB上知x+2kx=2,
得x=
 .
.所以
 .
.(3)根据点到直线的距离公式知,
点E,F到AB的距离分别为
h1=
 ,
,又|AB|=
 =
= ,
,所以四边形AEBF的面积为
S=

 .
.当2k=1,即当k=

 .
.点评:本题考查直线和椭圆的综合应用,解题时要认真审题,注意挖掘题中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
 已知椭圆
已知椭圆 的一个焦点到长轴的两个端点的距离分别为
的一个焦点到长轴的两个端点的距离分别为 和
和 ,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E,F两点.
,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E,F两点. ,求k的值;
,求k的值;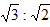 的两段,求其离心率;
的两段,求其离心率;  的一个焦点到长轴的两个端点的距离分别为
的一个焦点到长轴的两个端点的距离分别为 和
和 ,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E,F两点.
,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E,F两点. ,求k的值;
,求k的值;