题目内容
设数列 中,若
中,若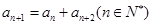 ,则称数列
,则称数列 为“凸数列”,已知数列
为“凸数列”,已知数列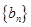 为 “凸数列”,且
为 “凸数列”,且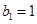 ,
,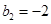 ,则数列
,则数列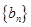 前2012项和等于 。
前2012项和等于 。
【答案】

【解析】
试题分析:根据题意可知, ,则数列
,则数列 为“凸数列”,那么当数列
为“凸数列”,那么当数列 为 “凸数列”, 且
为 “凸数列”, 且 ,
, ,可知
,可知
同理得到 ,可知数列的周期为6,那么求解的前6项的和为0,那么前2012项的和为335个周期的和加上数列的前两项的和,即为-1,故答案为-1.
,可知数列的周期为6,那么求解的前6项的和为0,那么前2012项的和为335个周期的和加上数列的前两项的和,即为-1,故答案为-1.
考点:本试题考查了数列的新定义的运用。
点评:解决该试题的关键是利用凸数列的定义,明确了任何一项如果始终等于前面和后面的相邻两项的和,则符合题意,进而发现数列的周期性,然后利用周期性来求解数列的前n项和的问题,属于中档题。

练习册系列答案
相关题目
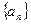 中,若
中,若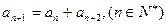 ,则称数列
,则称数列 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;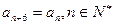 ;
;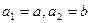 ,若数列
,若数列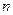 项和
项和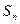 。
。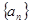 中,若
中,若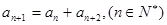 ,则称数列
,则称数列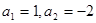 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;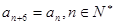 ;
;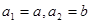 ,若数列
,若数列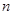 项和
项和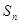 .
.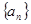 中,若
中,若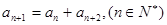 ,则称数列
,则称数列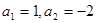 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;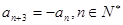 ;
;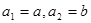 ,若数列
,若数列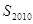 。
。