题目内容
(本小题满分12分)设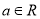 ,函数
,函数 .
.
(1)若函数 的图象在
的图象在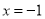 处的切线与直线
处的切线与直线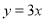 平行,求
平行,求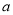 的值;
的值;
(2)若 ,求函数
,求函数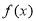 的极值与单调区间;
的极值与单调区间;
(3)若函数 的图象与直线
的图象与直线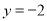 有三个公共点,求
有三个公共点,求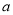 的取值范围.
的取值范围.
(1)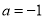 ;
;
(2)极小值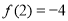 ,极大值
,极大值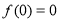 ;单调减区间为
;单调减区间为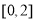 ,单调增区间为
,单调增区间为 和
和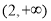 ;
;
(3)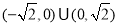 ;
;
【解析】
试题分析:(1)由题可知,函数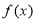 的图象在
的图象在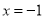 处的切线与直线
处的切线与直线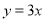 平行,则有
平行,则有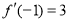 ,于是
,于是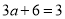 ,即
,即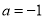 ;(2)若
;(2)若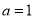 ,
,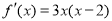 ,令
,令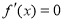 ,解得
,解得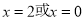 ,列出表格即可得到单调区间以及最值;(3)采用数形结合的方法求解,对a进行分情况讨论,当a=0时,不满足题意,当a>0时,让其最小值小于-2即可,当a<0时,让其最小值小于-2即可,故取并集得出a的取值范围;
,列出表格即可得到单调区间以及最值;(3)采用数形结合的方法求解,对a进行分情况讨论,当a=0时,不满足题意,当a>0时,让其最小值小于-2即可,当a<0时,让其最小值小于-2即可,故取并集得出a的取值范围;
试题解析:
(1)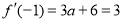 ,所以
,所以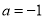 ,此时,切点为
,此时,切点为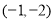 ,切线方程为
,切线方程为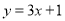 ,它与已知直线平行,符合题意. 2分
,它与已知直线平行,符合题意. 2分
(2)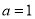 时,
时,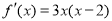 ,
,
当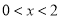 时,
时,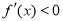 ,当
,当 ,或
,或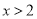 时,
时,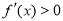 ,
,
所以,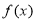 的单调减区间为
的单调减区间为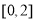 ,单调增区间为
,单调增区间为 和
和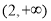 ; 4分
; 4分
当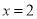 时,
时,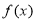 有极小值
有极小值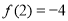 ,
,
当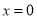 时,
时,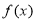 有极大值
有极大值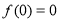 6分
6分
(3)当 时,
时,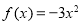 ,它与
,它与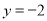 没有三个公共点,不符合题意 7分
没有三个公共点,不符合题意 7分
当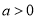 时,由
时,由 知,
知,
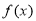 在
在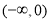 和
和 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
又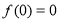 ,
, ,所以
,所以 ,即
,即 ,
,
又因为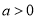 ,所以
,所以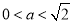 ; 9分
; 9分
当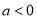 时,由
时,由 知,
知,
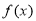 在
在 和
和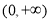 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
又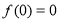 ,
, ,所以
,所以 ,即
,即 ,
,
又因为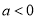 ,所以
,所以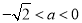 ; 11分
; 11分
综上所述,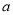 的取值范围是
的取值范围是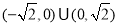 12分
12分
考点:导数的性质数形结合的应用
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的实数根的个数为 ( )
的实数根的个数为 ( )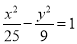 的左支上一点M到右焦点F2的距离为18,N是线段MF2的中点,O是坐标原点,则|ON|等于( )
的左支上一点M到右焦点F2的距离为18,N是线段MF2的中点,O是坐标原点,则|ON|等于( )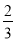
 的值为3,则输出
的值为3,则输出 的值是 .
的值是 .
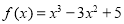 的单调减区间是( )
的单调减区间是( )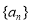 为等比数列,其中
为等比数列,其中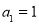 ,且
,且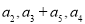 成等差数列.
成等差数列.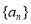 的通项公式;
的通项公式;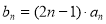 ,求数列
,求数列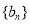 的前
的前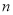 项和
项和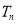 .
.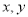 满足约束条件
满足约束条件 ,若目标函数
,若目标函数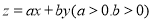 的最大值为12,则
的最大值为12,则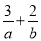 的最小值为( )
的最小值为( )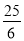 B.
B.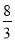 C.
C.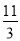 D.4
D.4 ,则下列结论正确的是: .
,则下列结论正确的是: . 的最小正周期为
的最小正周期为 ;
; 对称;
对称; ,0)对称;
,0)对称; 个单位,得到一个偶函数的图像;
个单位,得到一个偶函数的图像;  上为单调递增函数。
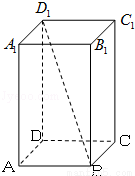
上为单调递增函数。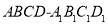 的底面是边长为1的正方形,侧棱长
的底面是边长为1的正方形,侧棱长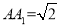 ,则异面直线
,则异面直线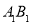 与
与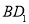 的夹角大小等于
的夹角大小等于