题目内容
(本小题满分10分)已知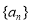 为等比数列,其中
为等比数列,其中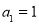 ,且
,且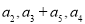 成等差数列.
成等差数列.
(1)求数列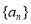 的通项公式;
的通项公式;
(2)设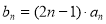 ,求数列
,求数列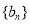 的前
的前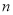 项和
项和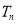 .
.
(1) (2)
(2)
【解析】
试题分析:(1)由题可知, 成等差数列,则根据等差中项的性质有
成等差数列,则根据等差中项的性质有 成立,再通过通项公式可变成关于q的方程,解方程得到公比
成立,再通过通项公式可变成关于q的方程,解方程得到公比 ;(2)将数列
;(2)将数列 的通项公式代入到数列
的通项公式代入到数列 中,得出
中,得出 ,为等差×等比形式,采用错位相减法求解前n项和;
,为等差×等比形式,采用错位相减法求解前n项和;
试题解析:(Ⅰ)∵ ,由通项公式
,由通项公式 ,得出
,得出 ;
;
∴公比 2分
2分
∵ ,且
,且 ,∴数列
,∴数列 的通项公式为
的通项公式为 5分
5分
(Ⅱ)∵ ,∴
,∴ .
.
∵ ,
,
∴
 ,..8分
,..8分
∴ 10分
10分
考点:等比数列的通项公式错位相减法求解数列的前n项和
考点分析: 考点1:等差数列 考点2:等比数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 是奇函数
是奇函数  的值;
的值; 的单调性,并用单调性定义证明;
的单调性,并用单调性定义证明; ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. C.
C. D.
D.
 ,
, ,
, ,...,以此类推,第5个等式为( )
,...,以此类推,第5个等式为( )



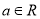 ,函数
,函数 .
. 的图象在
的图象在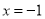 处的切线与直线
处的切线与直线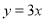 平行,求
平行,求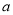 的值;
的值; ,求函数
,求函数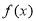 的极值与单调区间;
的极值与单调区间;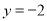 有三个公共点,求
有三个公共点,求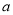 的取值范围.
的取值范围. 满足,且当
满足,且当 时,
时, ,函数
,函数 ,则函数
,则函数 在区间
在区间 内的零点的个数为( )
内的零点的个数为( ) ”是“直线
”是“直线 和直线
和直线  相互平行”的( )
相互平行”的( ) ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、
 ,直线
,直线 将△
将△ 分割为面积相等的两部分,则
分割为面积相等的两部分,则 ( )
( ) B.
B. C.
C. D.
D. 