题目内容
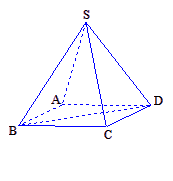
如图，四棱锥S- ABCD中，底面ABCD为平行四边形，E是SA上一点，试探求点E的位置，使SC//平面EBD，并证明．
答：点E的位置是 ．
证明：
中点
解析:
点E的位置是 棱SA的中点 ．
证明：取SA的中点E，连结EB，ED，AC，设AC与BD的交点为O，连结EO．
∵四边形ABCD是平行四边形，
∴点O是AC的中点．
又E是SA的中点，∴OE是ΔSAC的中位线．
∴OE//SC．
∵SC
平面EBD，OE
平面EBD，
∴SC//平面EBD．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
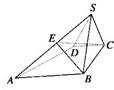如图，四棱锥S-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=SB=SC=2CD=2，侧面SBC⊥底面ABCD．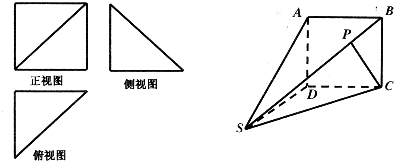
如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，点E是SD上的点，且DE=λa（0＜λ≤1）
如图，四棱锥S-ABCD的底面是矩形，AB=a，AD=2，SA=1，且SA⊥底面ABCD，若边BC上存在异于B，C的一点P，使得