Question

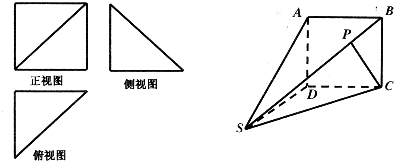
如图，四棱锥S-ABCD的正视图是边长为2的正方形，侧视图和俯视图是全等的等腰三角形，直线边长为2．
（1）求二面角C-SB-A的大小；
（2）P为棱SB上的点，当SP的长为何值时，CP⊥SA？

Answer 1

分析：（1）分别以DS、DC、DA所在直线为x、y、z轴建立直角坐标系，得出平面SBC的一个法向量

m

=(1，1，0)，且平面SAB的一个法向量

n

=(1，0，1)，利用空间向量的夹角公式，算出

m

、

n

夹角的余弦值，结合二面角C-SB-A是钝二面角，可得二面角C-SB-A大小；
（2）算出向量

SB

=（-2，2，2），设

SP

=k

SB

=(-2k，2k，2k)，根据CP⊥SA得

CP

•

SA

=0，建立关于k的方程解出k=

1

2

，从而算出

SP

=(-1，1，1)，得|

SP

|=

3

，即可得到CP⊥SA时SP的长．

解答：解（1）以D为坐标原点，分别以DS、DC、DA所在直线为x轴、y轴、z轴
建立空间直角坐标系．根据题意可得
平面SBC的一个法向量

m

=(1，1，0)（1分）
∵平面SAB的一个法向量

n

=(1，0，1)（2分）
∴cos＜

m

，

n

＞=

1

2

，得＜

m

，

n

＞=

π

3

（3分）
由图形观察，可得二面角C-SB-A是钝二面角，
因此二面角C-SB-A大小为

2π

3

（4分）
（2）由（1），可得S（2，0，0），
B（0，2，2），C（0，2，0），A（0，0，2）
设

SP

=k

SB

=(-2k，2k，2k)，k∈R（5分）
∴

CP

•

SA

=8k-4（6分）
∵CP⊥SA，∴

CP

•

SA

=0，可得k=

1

2

（7分）
因此，

SP

=(-1，1，1)，得|

SP

|=

3

，
即当SP的长为

3

时，CP⊥SA．（8分）

点评：本题在特殊四棱锥中求二面角的大小，并探索异面直线垂直的问题．着重考查了利用空间坐标系研究线线角、线面角和二面角大小等知识，考查了空间向量的数量积与向量的夹角公式，属于中档题．