题目内容

18．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的函数是（　　）
A．y=lnxB．y=x3C．$y={（\frac{1}{2}）^x}$D．y=sinx

分析 根据奇函数的定义，以及y=sinx，y=x3的图象即可找到既是奇函数又在（0，+∞）上单调递增的函数．

解答 解：y=lnx，$y=（\frac{1}{2}）^{x}$都是非奇非偶函数；
根据奇函数的定义及函数y=x3的图象知该函数为奇函数，且在（0，+∞）上单调递增，所以B正确；
y=sinx在（0，+∞）上没有单调性．
故选：B．

点评 考查奇函数定义，奇函数定义域及图象的特点，熟悉函数y=x3，y=sinx的图象，以及根据图象判断函数的单调性．

练习册系列答案
相关题目
11．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），F1、F2为左右焦点，B为短轴端点，且S${\;}_{△B{F}_{1}{F}_{2}}$=4，离心率为$\frac{\sqrt{2}}{2}$，O为坐标原点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆C恒有两个交点M、N，且满足|$\overrightarrow{OM}$+$\overrightarrow{ON}$|=|$\overrightarrow{OM}$-$\overrightarrow{ON}$|？若存在，求出该圆的方程，若不存在，说明理由．
11．若f（x）=x2，?t∈R，对于?x∈[2，m]，都有f（x+t）≤2x成立，则m的最大值是8．
7．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上单调递减，若实数a满足$f（{log_2}a）+f（{log_{\frac{1}{2}}}a）≤2f（1）$，则实数a的取值范围是（　　）
A．（0，2]B．$[\frac{1}{2}，2]$C．[2，+∞）D．$（0，\frac{1}{2}]∪[{2，+∞}）$
13．已知向量$\overrightarrow{a}$、$\overrightarrow{b}$均为单位向量，且|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{3}$，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（　　）
A．60°B．90°C．120°D．135°
3．已知向量$\overrightarrow{a}$=（sin2x，cosx），$\overrightarrow{b}$=（1，-2cosx），则函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$的最小正周期为π．
10．已知数列{an}满足log3an+1=log3an+1（n∈N），且a2+a4+a6=9，则logb（a5+a7+a9）的值等于5．
7．设f（x）是周期为4的周期函数，且当x∈（-1，3]时，$f（x）=\left\{{\begin{array}{l}{m\sqrt{1-{x^2}}，\;\;\;\;\;-1＜x≤1}\\{1-|{x-2}|，\;\;\;\;\;\;\;\;1＜x≤3}\end{array}}\right.$，若函数g（x）=3f（x）-x有且仅有五个零点，则正实数m的取值范围是（$\frac{\sqrt{15}}{3}$，$\sqrt{7}$）．
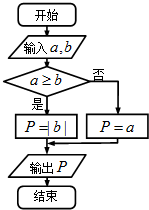5．定义一种运算符号“→”，两个实数a，b的“a→b”运算原理如图所示，若函数f（x）=2→x，则f（2）+f（-2）=（　　）
A．-2B．0C．2D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网