题目内容
13.求下列极限;(1)$\underset{lim}{x→1}$(2x2-1);
(2)$\underset{lim}{x→0}$$\frac{3x-1}{2x+3}$;
(3)$\underset{lim}{x→1}\sqrt{3x+1}$;
(4)$\underset{lim}{x→\frac{π}{6}}tanx$.
分析 将x的值代入多项式,即可求得各个多项式的极限值.
解答 解:(1)原式=$\underset{lim}{n→1}(2×{1}^{2}-1)=1$
(2)原式=$\underset{lim}{n→0}=\frac{3×0-1}{2×0+3}=-\frac{1}{3}$
(3)原式=$\underset{lim}{n→1}\sqrt{3×1+1}=2$
(4)原式=$\underset{lim}{n→\frac{π}{6}}=tan\frac{π}{6}=\frac{\sqrt{3}}{3}$
点评 本题求解函数的极限,解题时要注意公式的正确运用,属于基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
4.下列有关命题的说法正确的是( )
| A. | 若“p∧(?q)”为真命题,则“p∧q”也为真命题 | |
| B. | “x=3”是“2x2-7x+3=0”成立的充分不必要条件 | |
| C. | 命题“?x∈R,均有x2-x+1>0”的否定是:“?x∈R,使得x2-x+1<0” | |
| D. | 线性回归方程$\hat y=\hat bx+\hat a$对应的直线一定经过其样本数据点(x1,y1),(x2,y2),…,(xn,yn)中的一个点 |
1.实数x,y满足条件$\left\{\begin{array}{l}{x+y-4≤0}\\{x-2y+2≥0}\\{x≥0,y≥0}\end{array}\right.$,则z=x-y-1的最小值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 3 |
8.甲乙丙三人站成一排,则甲丙不相邻的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
5.“-1<x<2”是“|x-2|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.若$\overrightarrow{a}$=(1,2),$\overrightarrow b=({m,1})$,若$\overrightarrow a$∥$\overrightarrow b$,则m=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
3.若全集U=R,集合A={x|x2-x-2≥0},B={x|log3(2-x)≤1},则A∩(∁UB)=( )
| A. | {x|x<2} | B. | {x|x<-1或x≥2} | C. | {x|x≥2} | D. | {x|x≤-1或x>2} |
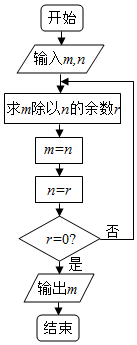 如图程序框图的算法思路源于古希腊数学家欧几里得的“辗转相除法”,执行该程序框图,若输入的m,n分别为153,119,则输出的m=( )
如图程序框图的算法思路源于古希腊数学家欧几里得的“辗转相除法”,执行该程序框图,若输入的m,n分别为153,119,则输出的m=( )