题目内容
设a，b是非负实数，求证：a3+b3≥
（a2+b2）．
| ab |
证明：由a，b是非负实数，作差得
a3+b3-
（a2+b2）=a2
（
-
）+b2
（
-
）
=（
-
）[（
）5-（
）5]．
当a≥b时，
≥
，从而（
）5≥（
）5，得（
-
）[（
）5-（
）5]≥0；
当a＜b时，
＜
，从而（
）5＜（
）5，得（
-
）[（
）5-（
）5]＞0．
所以a3+b3≥
（a2+b2）．
a3+b3-
| ab |
| a |
| a |
| b |
| b |
| b |
| a |
=（
| a |
| b |
| a |
| b |
当a≥b时，
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
当a＜b时，
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
所以a3+b3≥
| ab |
练习册系列答案
阅读快车系列答案
相关题目
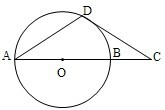本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．