题目内容
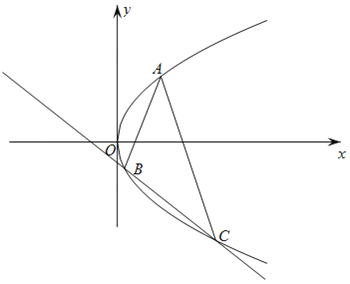
【题目】已知椭圆
的长轴是短轴的两倍，以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
，直线l与椭圆C交于
两点，其中直线l不过原点.
（1）求椭圆C的方程；
（2）设直线
的斜率分别为
，其中
且
.记
的面积为S.分别以
为直径的圆的面积依次为
，求
的最小值.
【答案】（1）
（2）
【解析】
（1）由题意知
，且
，由此能求出椭圆方程．
（2）设直线
的方程为
，
，
，
，
，联立
，利用韦达定理、椭圆弦长公式结合已知条件能求出
的最小值．
解：（1）由题意知，
，解得
，
所以椭圆C的方程为
（2）设直线l的方程为
，，，，，
由消去y整理得
，根据题设有：
且
，
.
因为
，所以
，
将，代入，化简得：
∵
，∴
.
此时
且
，解得
.故
，
又
，为定值.
∴
，
当且仅当
即
时等号成立.
综上：的最小值为
练习册系列答案
阅读快车系列答案
相关题目
【题目】某网购平台为了解某市居民在该平台的消费情况，从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名，并绘制如图所示频率分布直方图，已知中间三组的人数可构成等差数列.
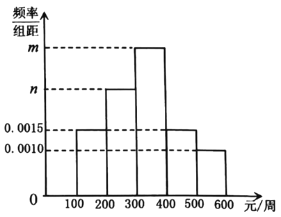
（1）求
的值；
（2）分析人员对100名调查对象的性别进行统计发现，消费金额不低于300元的男性有20人，低于300元的男性有25人，根据统计数据完成下列
列联表，并判断是否有
的把握认为消费金额与性别有关？
（3）分析人员对抽取对象每周的消费金额
与年龄
进一步分析，发现他们线性相关，得到回归方程
.已知100名使用者的平均年龄为38岁，试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.（同一组数据用该区间的中点值代替）
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
，其中
