题目内容
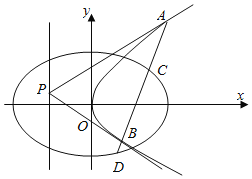
【题目】已知椭圆
的焦距为2，过点
.
（1）求椭圆
的标准方程；
（2）设椭圆的右焦点为F，定点
，过点F且斜率不为零的直线l与椭圆交于A，B两点，以线段AP为直径的圆与直线
的另一个交点为Q，证明：直线BQ恒过一定点，并求出该定点的坐标.
【答案】（1）
；（2）证明见解析，
.
【解析】
（1）根据题意列方程组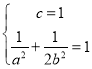
，求解
，
，即可.
（2）设
，
因为直线
的斜率不为零，令的方程为：
，与椭圆方程联立，得到
，
，由题意可知，
，则
，确定
的方程，由椭圆的对称性，则定点必在
轴上，所以令
，求解，即可.
（1）由题知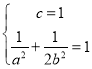 ， 解得
，
，
所以椭圆
的方程为；
（2）设，因为直线的斜率不为零，令的方程为：
，
由
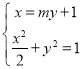得
，
则，，
因为以
为直径的圆与直线
的另一个交点为
,所以，则，
则
，故的方程为：
，
由椭圆的对称性，则定点必在轴上，所以令，则
，
而，，
，
所以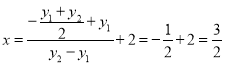
，
故直线恒过定点，且定点为.
练习册系列答案
相关题目
【题目】德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程，要求初等代数、初等几何都要合格，且初等数论和微积分初步至少有一门合格，则能取得参加数学竞赛复赛的资格，现有甲、乙、丙三位同学报名参加数学竞赛培训，每一位同学对这四门课程考试是否合格相互独立，其合格的概率均相同，（见下表），且每一门课程是否合格相互独立，
课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
合格的概率 |
|
|
|
|
（1）求甲同学取得参加数学竞赛复赛的资格的概率；
（2）记
表示三位同学中取得参加数学竞赛复赛的资格的人数，求
的分布列及期望
．
