题目内容
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
(Ⅰ)D在AC上运动,当D在何处时,有AB1∥平面BDC1,并且说明理由;
(Ⅱ)当AB1∥平面BDC1时,求二面角C-BC1-D余弦值.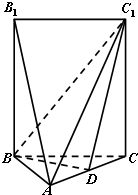
(Ⅰ)D在AC上运动,当D在何处时,有AB1∥平面BDC1,并且说明理由;
(Ⅱ)当AB1∥平面BDC1时,求二面角C-BC1-D余弦值.

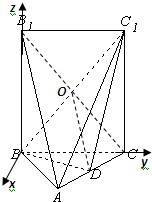
(Ⅰ)当D为AC中点时,有AB1∥平面BDC1,
证明:连接B1C交BC1于O,连接DO∵四边形BCC1B1是矩形
∴O为B1C中点又D为AC中点,从而DO∥AB,
∵AB1?平面BDC1,DO?平面BDC1∴AB1∥平面BDC1
(Ⅱ)建立空间直角坐标系B-xyz如图所示,则B(0,0,0),A(
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
所以
| BD |
| ||
| 2 |
| 3 |
| 2 |
| BC1 |
| 3 |
设
| n1 |
|
|
令Z=1,可得平面BDC1的一个法向量为
| n1 |
| 3 |
而平面BCC1的一个法向量为
| n2 |
所以cos<
| n1 |
| n2 |
| ||||
|
|
| 3 | ||
|
3
| ||
| 13 |
3
| ||
| 13 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
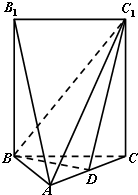 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.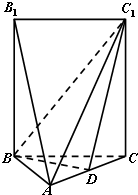 如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角.
如图,五面体A-BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A-BC-C1为直二面角. 如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图:五面体A-BCC1B1中,AB1=4,△ABC 是正三角形,AB=2,四边形 BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.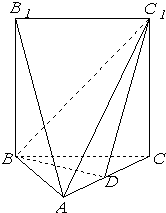 如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.
如图,五面体A-BCC1B1中,AB1=4,底面ABC是正三角形,AB=2,四边形BCC1B1是矩形,二面角A-BC-C1为直二面角,D为AC的中点.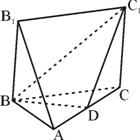 (1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;
(1)求证:AB1∥面BDC1;(2)求二面角C-BC1-D的大小;