题目内容

（本题满分12分）如图，五面体A－BCC1B1中，AB1＝4，底面ABC是正三角形，AB＝2，四边形BCC1B1是矩形，二面角A－BC－C1为直二面角，D为AC中点.

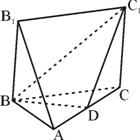（1）求证：AB1∥面BDC1；（2）求二面角C－BC1－D的大小；

（3）若A、B、C、C1为某一个球面上四点，求球的半径.

(Ⅰ)  略  (Ⅱ)    （Ⅲ）


解析:

（1）连B1C与BC1交于点O，则在△B1AC中，AB1∥OD

OD面BDC1　∴AB1∥面BDC1………………………………3分

（2）过D作DH⊥BC，则DH⊥面CBC1．过H作HQ⊥BC1

连DQ，由三垂线定理知DQ⊥BC1

∴∠DQH为二面角的平面角，……5分

 ∴二面角的大小为…………8分

（3）……12分

练习册系列答案
相关题目

（本题满分12分）

如图所示的几何体是由以正三角形为底面的直棱柱被平面所截而得. ，为的中点．

（1）当时，求平面与平面的夹角的余弦值；

（2）当为何值时，在棱上存在点，使平面？

 

（本题满分12分）如图，在长方体中，已知上下两底面为正方形，且边长均为1；侧棱，为中点，为中点，为上一个动点.

（Ⅰ）确定点的位置，使得；

（Ⅱ）当时，求二面角的平

面角余弦值.

 

（本题满分12分）如图，在四棱锥P—ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD=AB=2，E是PB的中点，F是AD的中点．

 ⑴求异面直线PD与AE所成角的大小；

 ⑵求证：EF⊥平面PBC ；

 ⑶求二面角F—PC—B的大小．.

 

 

 

（本题满分12分）

如图3，在圆锥中，已知的直径的中点．

（I）证明：

（II）求直线和平面所成角的正弦值．

 

 

（本题满分12分）

如图，三棱锥S—ABC中，AB⊥BC，D、E分别为AC、BC的中点，SA=SB=SC。

   （1）求证：BC⊥平面SDE；

   （2）若AB=BC=2，SB=4，求三棱锥S—ABC的体积。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网