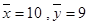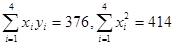题目内容
机器按照模具生产的产品有一些也会有缺陷,我们将有缺陷的产品称为次品,每小时出现的次品数随机器运转速度的不同而变化.下表为某机器生产过程的数据:
①求机器运转速度与每小时生产有缺点的产品数之间的回归方程.
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度每秒不超过多少百转?(写出满足的整数解).
| 速度x(百转/秒) | 每小时生产次品数y(个) |
| 2 | 30 |
| 4 | 40 |
| 5 | 50 |
| 6 | 60 |
| 8 | 70 |
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度每秒不超过多少百转?(写出满足的整数解).
分析:①先计算
,
,
xi2,
xiyi,再利用公式,即可求得回归直线方程;
②利用回归直线方程,建立不等式,即可求得机器的速度.
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
②利用回归直线方程,建立不等式,即可求得机器的速度.
解答:解:①
=
(2+4+5+6+8)=5,
=
(30+40+50+60+70)=50,
xi2=22+42+52+62+82=145,
xiyi=2×30++4×40+5×50+6×60+8×70=1390
∴
=
=7,
=
-
=50-7×5=15,…(7分)
∴回归直线方程为
=7x+15. …(8分)
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,则
≤75
即7x+15≤75解得x≤8.57…(10分)
∴实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度应每秒不超过8百转 …(12分)
. |
| x |
| 1 |
| 5 |
. |
| y |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
∴
 |
| b |
| 1390-5×5×50 |
| 145-5×52 |
 |
| a |
. |
| y |
 |
| b |
. |
| x |
∴回归直线方程为
 |
| y |
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,则
| ? |
| y |
即7x+15≤75解得x≤8.57…(10分)
∴实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度应每秒不超过8百转 …(12分)
点评:本题考查回归直线方程,考查学生的计算能力,考查利用数学知识解决实际问题,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
机器按照模具生产的产品有一些也会有缺陷,我们将有缺陷的产品称为次品,每小时出现的次品数随机器运转速度的不同而变化。下表为某机器生产过程的数据:
|
速度x(百转/秒) |
每小时生产次品数y(个) |
|
2 |
30 |
|
4 |
40 |
|
5 |
50 |
|
6 |
60 |
|
8 |
70 |
①求机器运转速度与每小时生产有缺点的产品数之间的回归方程
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度每秒不超过多少百转?(写出满足的整数解)
一机器可以按各种不同速度运转,其生产的产品有一些会有缺点,每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据:
|
速度(x转/秒) |
|
||
|
8 |
6 |
||
|
9 |
8 |
||
|
10 |
10 |
||
|
13 |
12 |
(1)、画出散点图;
(2)、求机器运转速度与每小时生产有缺点的产品数之间的回归方程;(系数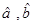 用分数表示)
用分数表示)
(3)、若实际生产所允许的每小时生产有缺点的产品数不超过10件,那么机器的速度每秒不超过多少转?
机器按照模具生产的产品有一些也会有缺陷,我们将有缺陷的产品称为次品,每小时出现的次品数随机器运转速度的不同而变化.下表为某机器生产过程的数据:
①求机器运转速度与每小时生产有缺点的产品数之间的回归方程.
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度每秒不超过多少百转?(写出满足的整数解).
| 速度x(百转/秒) | 每小时生产次品数y(个) |
| 2 | 30 |
| 4 | 40 |
| 5 | 50 |
| 6 | 60 |
| 8 | 70 |
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度每秒不超过多少百转?(写出满足的整数解).