题目内容
如图,已知正△A1B1C1 的边长是1,面积是P1,取△A1B1C1 各边的中点A2,B2,C2,△A2B2C2 的面积为P2,再取△A2B2C2 各边的中点A3,B3,C3,△A3B3C3 的面积为P3,依此类推.记Sn=P1+P2+…+Pn
,则
Sn ( )

,则
| lim |
| n→∞ |
A.
| B.
| C.2
| D.4
|

∵正△A1B1C1 的边长是1,
∴面积是P1=
×12,
取△A1B1C1各边的中点A2,B2,C2,则△A2B2C2 的边长为
,
其面积为P2=
×(
)2,
再取△A2B2C2 各边的中点A3,B3,C3,则△A3B3C3 的边长为
,
其面积为P3=
×(
)2,
…
依此类推得Pn=
×[(
)n-1]2,
∵Sn=P1+P2+…+Pn,
∴Sn=
×12+
×(
)2+
×(
)2+…+
×[(
)n-1]2
=
{ [12+ (
)2+(
)2+…+[(
)n-1]2 }=
×
,
∴
Sn=
×
=
×
=
.
故选A.
∴面积是P1=
| ||
| 4 |
取△A1B1C1各边的中点A2,B2,C2,则△A2B2C2 的边长为
| 1 |
| 2 |
其面积为P2=
| ||
| 4 |
| 1 |
| 2 |
再取△A2B2C2 各边的中点A3,B3,C3,则△A3B3C3 的边长为
| 1 |
| 4 |
其面积为P3=
| ||
| 4 |
| 1 |
| 4 |
…
依此类推得Pn=
| ||
| 4 |
| 1 |
| 2 |
∵Sn=P1+P2+…+Pn,
∴Sn=
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
=
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
1•[1-(
| ||
1-
|
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| ||
| 4 |
1•[1-(
| ||
1-
|
| ||
| 4 |
| 1 | ||
1-
|
| ||
| 3 |
故选A.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
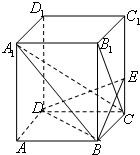 如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,
如图,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,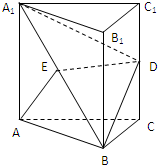 如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点.
如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点. 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点. 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.