题目内容
已知向量m= (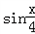 ,
,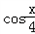 ),n=(
),n=(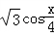 ,
,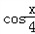 ),记f(x)=m·n;
),记f(x)=m·n;
(1)若f(x)=1,求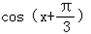 的值;
的值;
(2)若△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围。
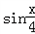 ,
,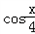 ),n=(
),n=(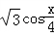 ,
,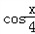 ),记f(x)=m·n;
),记f(x)=m·n;(1)若f(x)=1,求
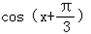 的值;
的值;(2)若△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围。
解:(1)f(x)=m·n= sin
sin =
= =sin(
=sin( )+
)+ ,
,
∵f(x)=1,
∴sin( )=
)= ,
,
∴cos(x+ )=1-2
)=1-2 =
= 。
。
(2)∵(2a-c)cosB=bcosC,
∴由正弦定理得(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0,
∴cosB= ,B=
,B= ;
;
0<A< ,
,
∴ ,
,
 ,
,
 ;
;
又∵f(x)=sin( )+
)+
∴f(A)=sin( )+
)+ ,
,
故函数f(A)的取值范围是(1, )。
)。
 sin
sin =
= =sin(
=sin( )+
)+ ,
,∵f(x)=1,
∴sin(
 )=
)= ,
,∴cos(x+
 )=1-2
)=1-2 =
= 。
。(2)∵(2a-c)cosB=bcosC,
∴由正弦定理得(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,
∴2sinAcosB=sin(B+C),
∵A+B+C=π,
∴sin(B+C)=sinA,且sinA≠0,
∴cosB=
 ,B=
,B= ;
;0<A<
 ,
,∴
 ,
,
 ,
, ;
;又∵f(x)=sin(
 )+
)+
∴f(A)=sin(
 )+
)+ ,
,故函数f(A)的取值范围是(1,
 )。
)。
练习册系列答案
相关题目