题目内容
 已知:如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥DE交CB延长线于点F.若
已知:如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥DE交CB延长线于点F.若 ,求EF的长.
,求EF的长.
解:设⊙P 的半径为 r,Rt△CBP中,由勾股定理得 8+r2=(2+r)2,
∴r=1. 由Rt△CBP和R t△CEF相似可得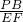 =
=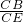 ,即
,即  =
= ,
,
∴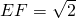 .
.
分析:Rt△CBP中,由勾股定理求得⊙P的半径BP,再由直角三角形CBP和CEF相似,对应边成比例得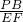 =
=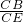 ,求出EF的长.
,求出EF的长.
点评:本题考查勾股定理的应用,三角形相似对应边成比例.
∴r=1. 由Rt△CBP和R t△CEF相似可得
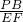 =
=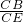 ,即
,即  =
= ,
,∴
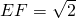 .
.分析:Rt△CBP中,由勾股定理求得⊙P的半径BP,再由直角三角形CBP和CEF相似,对应边成比例得
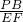 =
=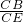 ,求出EF的长.
,求出EF的长.点评:本题考查勾股定理的应用,三角形相似对应边成比例.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知:如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥DE交CB延长线于点F.若
已知:如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥DE交CB延长线于点F.若 交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长
交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长 线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2
线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=2 ,求E
,求E F的长.
F的长.
 ,求EF的长.
,求EF的长.
 ,求EF的长.
,求EF的长. ,求EF的长.
,求EF的长.