题目内容
已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]() ,
,
(I)求![]() 与
与![]() 的关系式;
的关系式;
(II)求![]() 的单调区间;
的单调区间;
(III)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于![]() ,求
,求![]() 的取值范围.
的取值范围.
(I)解![]()
因为![]() 是函数
是函数![]() 的一个极值点,所以
的一个极值点,所以![]() ,
,
所以![]()
(II)由(I)知,![]() .
.
当![]() 时,有
时,有![]() ,当
,当![]() 变化时,
变化时,![]() 与
与![]() 的变化如下表:
的变化如下表:
|
|
|
|
| 1 |
|
|
| <0 | 0 | >0 | 0 | <0 |
|
| 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
由上表知,当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
(III)解法一:
由已知,得![]() ,即
,即![]()
∵![]() ,
,
∴![]()
即![]()
![]() (*)
(*)
设![]() ,其函数图象的开口向上,
,其函数图象的开口向上,
由题意(*)式恒成立,∴

∴.![]()
即![]() 的取值范围为
的取值范围为![]()
解法二:由已知,得![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]()
![]() (*)
(*)
1* x=1时,(*)式化为0<1恒成立,∴![]() 。
。
2* x≠1时,∵![]() ∴
∴![]()
(*)式化为![]()
令t= x-1,则t∈[-2,0),记![]()
则g(t)在区间[-2,0)是单调增函数。
∴![]()
由(*)式恒成立,必有![]() ,
,
∴![]()
综上1*、2*知![]()

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 与
与 的关系式;
的关系式; 的单调区间;
的单调区间;
 ;试比较g(x)与
;试比较g(x)与 的大小。
的大小。 是函数
是函数 的一个极值点.
的一个极值点.
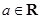

 的值;
的值; ,
, 时,证明:
时,证明:
 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与 的关系式;
的关系式;  的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求
,求 的取值范围.
的取值范围. 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 。
。 与
与 的关系表达式;
的关系表达式; 的单调区间;
的单调区间; 时,函数
时,函数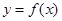 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求实数
,求实数 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与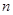 的关系式;
的关系式; 的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3