题目内容
已知 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
,
(1)求 与
与 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当 时,函数
时,函数 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求
,求 的取值范围.
的取值范围.
【答案】
(1) 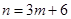 ;(2)当
;(2)当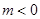 时,
时,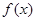 在
在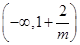 单调递减,在
单调递减,在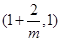 单调递增,在
单调递增,在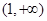 上单调递减.(3)
上单调递减.(3)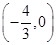
【解析】
根据导数在函数中的应用,x=1时,导数为0 ,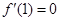 ,即
,即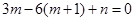 ;
;
(2)由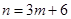 ,求
,求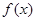 的单调区间时,减少变量,解析式是
的单调区间时,减少变量,解析式是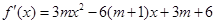 ,分类讨论导数为正、负时的x范围;
,分类讨论导数为正、负时的x范围;
函数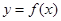 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于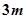 即
即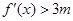 从而
从而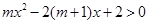 ,转化为二次函数定区间动轴问题。
,转化为二次函数定区间动轴问题。
解:(1)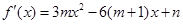 因为
因为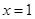 是函数
是函数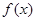 的一个极值点,
的一个极值点,
所以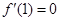 ,即
,即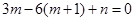 ,所以
,所以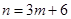
(2)由(1)知,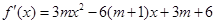 =
=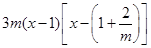
当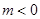 时,有
时,有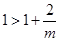 ,当
,当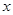 变化时,
变化时,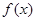 与
与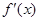 的变化如下表:
的变化如下表:
|
|
|
|
|
1 |
|
|
|
|
0 |
|
0 |
|
|
|
调调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
故有上表知,当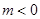 时,
时,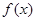 在
在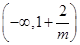 单调递减,
单调递减,
在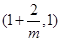 单调递增,在
单调递增,在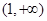 上单调递减.
上单调递减.
(3)由已知得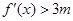 ,即
,即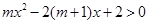
又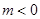 所以
所以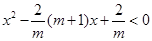 即
即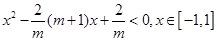 ①
①
设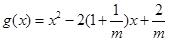 ,其函数开口向上,由题意知①式恒成立,
,其函数开口向上,由题意知①式恒成立,
所以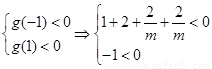 解之得
解之得
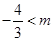 又
又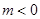
所以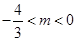
即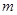 的取值范围为
的取值范围为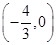

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
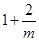
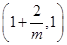
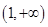
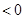
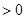
 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 与
与 的关系式;
的关系式; 的单调区间;
的单调区间;
 ;试比较g(x)与
;试比较g(x)与 的大小。
的大小。 是函数
是函数 的一个极值点.
的一个极值点.
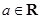

 的值;
的值; ,
, 时,证明:
时,证明:
 是函数
是函数 的一个极值点,其中
的一个极值点,其中
 。
。 与
与 的关系表达式;
的关系表达式; 的单调区间;
的单调区间; 时,函数
时,函数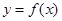 的图象上任意一点的切线斜率恒大于
的图象上任意一点的切线斜率恒大于 ,求实数
,求实数 是函数
是函数 的一个极值点,其中
的一个极值点,其中 ,
, 与
与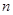 的关系式;
的关系式; 的单调区间;
的单调区间; 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3