Question

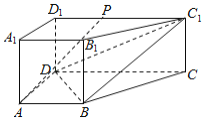
【题目】如图,四棱柱中,底面,底面是梯形,AB//DC,,

(1).求证:平面平面;

(2)求二面角的平面角的正弦值

(3).在线段上是否存在一点,使AP//平面.若存在,请确定点的位置;若不存在,请说明理由.

Answer 1

【答案】（1）证明见解析；（2）；（3）存在点是的中点，使平面，证明见解析.

【解析】

（1）根据面面垂直的判定定理即可证明平面平面；

（2）由（1）知，且平面，可知为二面角的平面角，在中利用勾股定理得到即可求得的正弦值；

（3）根据线面平行的判定定理进行证明即可得到结论．

证明：（1）因为底面，所以底面，

因为底面，

所以，

因为底面是梯形，，，

，

因为，所以，

所以，，

所以在中，，

所以，

所以，

又因为，

所以平面，

因为平面，

所以平面平面，

（2）由（1）知，且平面，则为二面角的平面角，

，

由勾股定理可得

即二面角的平面角的正弦值为.

（3）存在点是的中点，使平面

证明如下：取线段的中点为点，连结，

所以，且

因为，，

所以，且

所以四边形是平行四边形．

所以．

又因为平面，平面，

所以平面．