题目内容
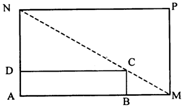 某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.
某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.(1)要使飞鸟恰巧停在矩形花园ABCD内的概率不大于
| 3 | 16 |
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求最小面积.
分析:(1)由题意设出AN的长为x米,因为三角形DNC∽三角形ANM,则对应线段成比例可知AM,表示出矩形AMPN的面积,然后根据飞鸟恰巧停在矩形花园ABCD内的概率不大于
,建立不等式,解之即可;
(2)利用a+b≥2
当且仅当a=b时取等号的方法求出S的最大值即可.
| 3 |
| 16 |
(2)利用a+b≥2
| ab |
解答:解:(1)设AN=x米,(x>2),则ND=x-2
∵
=
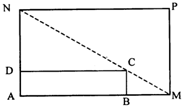
∴
=
∴AM=
…2 分
故飞鸟停在小花园中的概率为P,P=
=
=
…4 分
由题意:
≤
…5 分
∴3x2-32x+64≥0 …(7分)
即(3x-8)(x-8)≥0
∴2<x≤
或x≥8 …(8分)
(2)SAMPN=
=
…(12分)
=3(x-2)+
+12 …(14分)
≥2
+12=24 …(15分)
此时x=4 当AN的长度是4米时,矩形AMPN的面积最小,最小面积为24米2. …(16分)
∵
| ND |
| DC |
| AN |
| AM |

∴
| x-2 |
| 3 |
| x |
| AM |
∴AM=
| 3x |
| x-2 |
故飞鸟停在小花园中的概率为P,P=
| SABCD |
| SAMPN |
| 6 | ||
|
| 2(x-2) |
| x2 |
由题意:
| 2(x-2) |
| x2 |
| 3 |
| 16 |
∴3x2-32x+64≥0 …(7分)
即(3x-8)(x-8)≥0
∴2<x≤
| 8 |
| 3 |
(2)SAMPN=
| 3x2 |
| x-2 |
| 3(x-2)2+12(x-2)+12 |
| x-2 |
=3(x-2)+
| 12 |
| x-2 |
≥2
| 36 |
此时x=4 当AN的长度是4米时,矩形AMPN的面积最小,最小面积为24米2. …(16分)
点评:考查学生会根据实际问题选择函数关系的能力,利用导数求闭区间上函数最值的能力.以及用a+b≥2
当且仅当a=b时取等号的方法求最值的能力.
| ab |

练习册系列答案
相关题目
 某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点
某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点
 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
. 为圆心的圆与主干道
为圆心的圆与主干道 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式; 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn. 是等差数列,并求|OAn|关于n的表达式;
是等差数列,并求|OAn|关于n的表达式; (单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
(单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
 将之扩建成一个再大些的矩形花园
将之扩建成一个再大些的矩形花园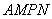 ,要求
,要求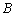 在
在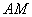 上,
上, 在
在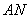 上,且对角线
上,且对角线 过
过 点,已知
点,已知 米,
米,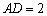 米.现有一飞鸟在矩形花园
米.现有一飞鸟在矩形花园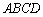 内的概率不大于
内的概率不大于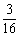 ,则
,则