题目内容
(本小题满分14分)某城市自西向东和自南向北的两条主干道的东南方位有一块空地市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,

其中, 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点
 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
.
(1)记以 为圆心的圆与主干道
为圆心的圆与主干道 切于
切于 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式;
(2)记 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 个圆型小道的修建?请说明你的理由.
个圆型小道的修建?请说明你的理由.
【答案】
(1)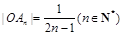 . (2) 5周内能完成前
. (2) 5周内能完成前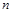 个圆型小道的修建工作.
个圆型小道的修建工作.
【解析】(1) 由题意知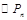 的半径
的半径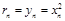 .再根据
.再根据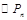 与
与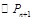 彼此相切,得
彼此相切,得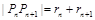 ,
,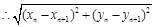 =
=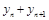 ,平方整理可证明结论.
,平方整理可证明结论.
(2) 由于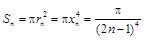 ,所以可得
,所以可得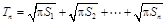 =
=
<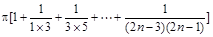
再裂项求和即可证明结论.
解:(1)依题设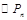 的半径
的半径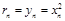 .
.
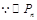 与
与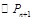 彼此相切,
彼此相切,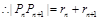 ,
,
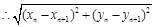 =
=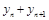 ,
,
两边平方整理得: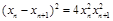 ,又
,又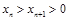 ,
,
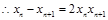 ,
,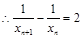 .
.
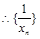 是等差数列,首项为1,公差为2.
是等差数列,首项为1,公差为2.
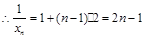 ,
,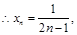 即
即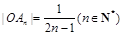 .…………………………8分
.…………………………8分
(2) ,
,
设前几个圆型小道的施工总工时为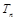
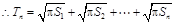 =
=
<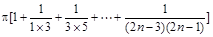
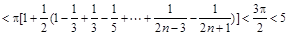 .
.
故5周内能完成前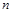 个圆型小道的修建工作.……………………14分
个圆型小道的修建工作.……………………14分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)