题目内容
某城市规划部门计划依托一矩形花园 将之扩建成一个再大些的矩形花园
将之扩建成一个再大些的矩形花园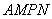 ,要求
,要求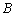 在
在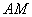 上,
上, 在
在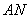 上,且对角线
上,且对角线 过
过 点,已知
点,已知 米,
米,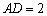 米.现有一飞鸟在矩形花园
米.现有一飞鸟在矩形花园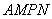 上空自由飞翔,并确定在花园
上空自由飞翔,并确定在花园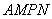 内休息.
内休息.
(1)要使飞鸟恰巧停在矩形花园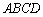 内的概率不大于
内的概率不大于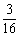 ,则
,则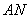 的长应在什么范围内?
的长应在什么范围内?
(2)当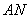 的长度是多少时,矩形
的长度是多少时,矩形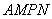 的面积最小?并求最小面积.
的面积最小?并求最小面积.

【答案】
解:(1)设 米,
米, ,则
,则
 ∵
∵
∴
∴ ……………2 分
……………2 分
故飞鸟停在小花园中的概率为 ,
,
 即
即
 ……………4 分
……………4 分
由题意:  ……………5 分
……………5 分
∴ ……………7分
……………7分
即
∴ 或
或 ……………8分
……………8分
(2)
 ……………12分
……………12分
 ……………14分
……………14分
 ……………15分
……………15分
此时 答略
……………16分
答略
……………16分

练习册系列答案
相关题目
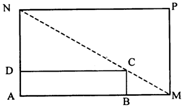 某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息.
某城市规划部门计划依托一矩形花园ABCD将之扩建成一个再大些的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=3米,AD=2米.现有一飞鸟在矩形花园AMPN上空自由飞翔,并确定在花园AMPN内休息. 某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点
某城市自西向东和自南向北的两条主干道的东南方位有一块空地,市规划部门计划利用它建设一个供市民休闲健身的小型绿化广场,如下图所示是步行小道设计方案示意图,其中,Ox,Oy分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点O处修一条步行小道,小道为抛物线y=x2的一段,在小道上依次以点
 分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点
分别表示自西向东,自南向北的两条主干道.设计方案是自主干道交汇点 处修一条步行小道,小道为抛物线
处修一条步行小道,小道为抛物线 的一段,在小道上依次以点
的一段,在小道上依次以点 为圆心,修一系列圆型小道,这些圆型小道与主干道
为圆心,修一系列圆型小道,这些圆型小道与主干道 相切,且任意相邻的两圆彼此外切,若
相切,且任意相邻的两圆彼此外切,若 (单位:百米)且
(单位:百米)且 .
. 为圆心的圆与主干道
为圆心的圆与主干道 点,证明:数列
点,证明:数列 是等差数列,并求
是等差数列,并求 关于
关于 的表达式;
的表达式; 的面积为
的面积为 ,根据以往施工经验可知,面积为
,根据以往施工经验可知,面积为 的圆型小道的施工工时为
的圆型小道的施工工时为 (单位:周).试问5周时间内能否完成前
(单位:周).试问5周时间内能否完成前 为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn.
为圆心,修一系列圆型小道,这些圆型小道与主干道Ox相切,且任意相邻的两圆彼此外切,若x1=1(单位:百米)且xn+1<xn. 是等差数列,并求|OAn|关于n的表达式;
是等差数列,并求|OAn|关于n的表达式; (单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.
(单位:周).试问5周时间内能否完成前n个圆型小道的修建?请说明你的理由.