题目内容
3.在等腰直角△ABC中,AB=AC=$\sqrt{2}$,D、E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是[$\frac{8}{9},\frac{4}{3}$].分析 可作出图形,分别以AC,AB为x轴,y轴,建立平面直角坐标系,根据条件即可设$D(x,\sqrt{2}-x),E(x+\frac{\sqrt{2}}{3},\frac{2\sqrt{2}}{3}-x)$,并且可求得$0≤x≤\frac{2\sqrt{2}}{3}$,从而进行数量积的坐标运算便可求出$\overrightarrow{AD}•\overrightarrow{AE}=2{x}^{2}-\frac{4\sqrt{2}}{3}x+\frac{4}{3}$,配方,根据x的范围即可求出$\overrightarrow{AD}•\overrightarrow{AE}$的最大值和最小值,即得出$\overrightarrow{AD}•\overrightarrow{AE}$的取值范围.
解答 解:如图,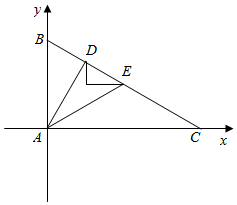
分别以AC,AB为x,y轴,建立平面直角坐标系;
∵$DE=\frac{1}{3}BC$,设$D(x,\sqrt{2}-x)$,$0≤x≤\frac{2\sqrt{2}}{3}$,则$E(x+\frac{\sqrt{2}}{3},\frac{2\sqrt{2}}{3}-x)$;
∴$\overrightarrow{AD}•\overrightarrow{AE}=(x,\sqrt{2}-x)•(x+\frac{\sqrt{2}}{3},\frac{2\sqrt{2}}{3}-x)$
=${x}^{2}+\frac{\sqrt{2}}{3}x+\frac{4}{3}-\sqrt{2}x-\frac{2\sqrt{2}}{3}x+{x}^{2}$
=$2{x}^{2}-\frac{4\sqrt{2}}{3}x+\frac{4}{3}$
=$2(x-\frac{\sqrt{2}}{3})^{2}+\frac{8}{9}$;
∴$x=\frac{\sqrt{2}}{3}$时,$\overrightarrow{AD}•\overrightarrow{AE}$取最小值$\frac{8}{9}$,x=0或$\frac{2\sqrt{2}}{3}$时,$\overrightarrow{AD}•\overrightarrow{AE}$取最大值$\frac{4}{3}$;
∴$\overrightarrow{AD}•\overrightarrow{AE}$的取值范围是$[\frac{8}{9},\frac{4}{3}]$.
故答案为:$[\frac{8}{9},\frac{4}{3}]$.
点评 考查通过建立平面直角坐标系,利用向量的坐标解决向量问题的方法,根据条件能设平面上点的坐标,根据点的坐标可求向量的坐标,以及向量数量积的坐标运算,配方求二次函数的最值.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | {0,1,2,3,4} | B. | {0,1,2} | C. | {0,2,4} | D. | {1,2} |