题目内容
(本题满分13分)如图,设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,焦点为
,焦点为![]() ;以
;以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆
的椭圆![]() 与抛物线
与抛物线![]() 在
在![]() 轴上方的交点为
轴上方的交点为![]() ,延长
,延长![]() 交抛物线于点
交抛物线于点![]() ,
,![]() 是抛物线
是抛物线![]() 上一动点,且M在
上一动点,且M在![]() 与
与![]() 之间运动.
之间运动.
(Ⅰ)当![]() 时,求椭圆
时,求椭圆![]() 的方程;ks*5u
的方程;ks*5u
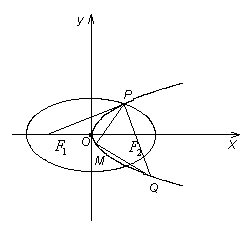 (Ⅱ)当
(Ⅱ)当![]() 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求![]() 面积的最大值.
面积的最大值.
解:(1)当![]() 时,
时, ![]() ,则
,则![]()
设椭圆方程为![]() ,则
,则![]() 又
又![]() ,所以
,所以![]()
所以椭圆C2方程为![]()
(2)因为![]() ,
,![]() ,则
,则![]() ,
,![]() ,设椭圆方程为
,设椭圆方程为![]()
由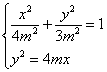 ,得
,得![]() 即
即![]() ,
,
得![]() 代入抛物线方程得
代入抛物线方程得![]() ,即
,即![]()
![]() ,
,![]() ,
,
因为![]() 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以![]()
此时抛物线方程为![]() ,
,![]() ,直线
,直线![]() 方程为:
方程为:![]() .
.
联立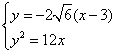 ,得
,得![]() ,即
,即![]() ,
,
所以![]() ,代入抛物线方程得
,代入抛物线方程得![]() ,即
,即![]()
∴![]() .
.
设![]() 到直线PQ的距离为
到直线PQ的距离为![]() ,
,![]()
则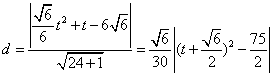
当![]() 时,
时,![]() ,
,
即![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在城
在城 的南偏西
的南偏西 的方向上,由
的方向上,由 ,在
,在 处,有一人正沿公路向
处,有一人正沿公路向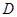 处,此时
处,此时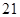 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达
 中,
中,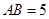 ,
, ,
, ,
, ,
, ,
, 是
是 的中点,设
的中点,设 ,
, ,
, .
.
 表示
表示 ;
; 的长.
的长.
 ,
, ,底面
,底面 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD,  ,O为AD中点.
,O为AD中点.
 与平面
与平面 所成角的余弦值;
所成角的余弦值; 点到平面
点到平面 的距离
的距离 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 中,已知
中,已知
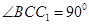 ,
,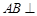 侧面
侧面

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).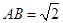 ,求二面角
,求二面角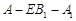 的大小.
的大小.