Question

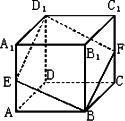
如图，已知E，F分别是正方体ABCD－A₁B₁C₁D₁的棱AA₁和棱CC₁上的点，且AE＝C₁F，求证：四边形EBFD₁是平行四边形．

Answer 1

答案：
解析：

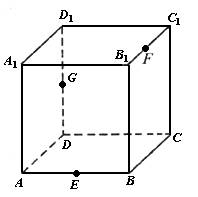
证明：如图，在棱DD1上取一点G，使D1G＝A1E． 　　又因为A1E∥D1G， 　　所以四边形A1EGD1为平行四边形， 　　所以EG∥A1D1，且EG＝A1D1． 　　又因为A1D1∥BC，且A1D1＝BC， 　　所以EG∥BC，且EG＝BC， 　　所以四边形EBCG为平行四边形， 　　所以EB∥GC，且EB＝GC． 　　又因为D1G＝A1E，AE＝C1F，AA1＝CC1， 　　所以D1G＝FC． 　　又因为D1G∥FC， 　　所以四边形D1GCF为平行四边形， 　　所以GC∥D1F，且GC＝D1F． 　　所以EB∥D1F，且EB＝D1F． 　　所以四边形EBFD1为平行四边形． 　　点评：对于空间几何中的两直线a，b，如果很难直接判断它们是否平行，可利用a∥c与b∥c证得(即运用公理4证明)．