题目内容
(1)已知方程x2-(2i-1)x+3m-i=0有实数根,求实数y=x(x-1)(x-2)的值.
(2)z∈C,解方程z•
-2zi=1+2i.
(2)z∈C,解方程z•
. | z |
分析:(1)设出方程x2-(2i-1)x+3m-i=0的实数根,代入后整理为a+bi(a,b∈R)=0的形式,由复数相等的条件列式求出实根,代入y=x(x-1)(x-2)化简即可.
(2)设z=a+bi(a,b∈R),代入方程z•
-2zi=1+2i,整理后利用复数相等的条件求解a,b的值,则复数z可求.
(2)设z=a+bi(a,b∈R),代入方程z•
. |
| z |
解答:解:(1)设方程的实根为x0,则x02-(2i-1)x0+3m-i=0,
因为x0、m∈R,所以方程变形为(x02+x0+3m)-(2x0+1)i=0,
由复数相等得
,解得
,
故y=x(x-1)(x-2)=(-
)(-
-1)(-
-2)=-
.
(2)设z=a+bi(a,b∈R),则(a+bi)(a-bi)-2i(a+bi)=1+2i,
即a2+b2+2b-2ai=1+2i.
由
,得
或
,
∴z=-1或z=-1-2i.
因为x0、m∈R,所以方程变形为(x02+x0+3m)-(2x0+1)i=0,
由复数相等得
|
|
故y=x(x-1)(x-2)=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 8 |
(2)设z=a+bi(a,b∈R),则(a+bi)(a-bi)-2i(a+bi)=1+2i,
即a2+b2+2b-2ai=1+2i.
由
|
|
|
∴z=-1或z=-1-2i.
点评:本题考查复数代数形式的混合运算,复数的分类,是中档题.

练习册系列答案
相关题目
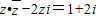 .
.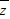 -2zi=1+2i.
-2zi=1+2i.