题目内容
(1)已知方程x2-(2i-1)x+3m-i=0有实数根,求实数m的值.
(2)z∈C,解方程z•
-2zi=1+2i.
(2)z∈C,解方程z•
. | z |
分析:(1)设方程的实根为x0,则x02-(2i-1)x0+3m-i=0,利用复数相等的条件,解方程组即可;
(2)设z=a+bi(a,b∈R),依题意可得a2+b2+2b-2ai=1+2i,利用两复数相等的条件,解方程组即可.
(2)设z=a+bi(a,b∈R),依题意可得a2+b2+2b-2ai=1+2i,利用两复数相等的条件,解方程组即可.
解答:解:(1)设方程的实根为x0,则x02-(2i-1)x0+3m-i=0,
因为x0、m∈R,所以方程变形为(x02+x0+3m)-(2x0+1)i=0,
由复数相等得
,解得
,
故m=-
.
(2)设z=a+bi(a,b∈R),则(a+bi)(a-bi)-2i(a+bi)=1+2i,
即a2+b2+2b-2ai=1+2i.
由
得
或
,
∴z=-1或z=-1-2i.
因为x0、m∈R,所以方程变形为(x02+x0+3m)-(2x0+1)i=0,
由复数相等得
|
|
故m=-
| 1 |
| 12 |
(2)设z=a+bi(a,b∈R),则(a+bi)(a-bi)-2i(a+bi)=1+2i,
即a2+b2+2b-2ai=1+2i.
由
|
|
|
∴z=-1或z=-1-2i.
点评:本题考查复数代数形式的混合运算,着重考查两复数相等的条件的应用,考查转化思想与方程思想及运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
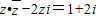 .
.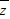 -2zi=1+2i.
-2zi=1+2i.