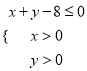题目内容

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，设倾斜角为的直线的参数方程为（为参数）与曲线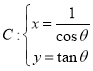（为参数）相交于不同的两点．

（1）若，求线段的中点的直角坐标；

（2）若直线的斜率为2，且过已知点，求的值．

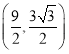【答案】（1）（2）

【解析】

试题分析：（1）根据，将参数方程转化为普通方程：，再将直线参数方程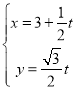代入，利用韦达定理得，最后根据直线参数方程几何意义得线段的中点对应参数为，即得线段的中点的直角坐标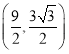（2）将直线参数方程（其中）代入，利用韦达定理得，最后根据直线参数方程几何意义得

试题解析：（1）由曲线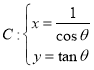（为参数），可得的普通方程是．．．．．．．．．．2分

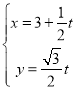当时，直线的参数方程为（为参数），

代入曲线的普通方程，得，．．．．．．．．．．．．．．．．．．3分

得，则线段的中点对应的，

故线段的中点的直角坐标为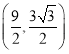．．．．．．．．．．．．．．．．．．．5分

（2）将直线的参数方程代入曲线的普通方程，化简得

，．．．．．．．．．．．．．．．．．．．．．．7分

则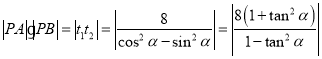，．．．．．．．．．．．．．．．．．．．．．．．9分

故已知得，故．．．．．．．．．．．．．．．．．．．．．．．10分

练习册系列答案
相关题目

【题目】某商场举行有奖促销活动，顾客购买一定金额商品后即可抽奖，每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中，各随机摸出1个球，在摸出的2个球中，若都是红球，则获一等奖；若只有1个红球，则获二等奖；若没有红球，则不获奖.

（1）求顾客抽奖1次能获奖的概率；

（2）若某顾客有3次抽奖机会，记该顾客在3次抽奖中获一等奖的次数为，求的分布列和数学期望.

【题目】已知函数.

（1）若曲线在点处与直线相切，求的值；

（2）若函数有两个零点，试判断的符号，并证明.

【题目】已知抛物线， 是焦点，直线是经过点的任意直线．

（Ⅰ）若直线与抛物线交于、两点，且（是坐标原点， 是垂足），求动点的轨迹方程；

（Ⅱ）若、两点在抛物线上，且满足，求证：直线必过定点，并求出定点的坐标．

【题目】函数．

（1）若函数在上为增函数，求的取值范围；

（2）若函数在上不单调时；

①记在上的最大值、最小值分别为，求；

②设，若，对恒成立，求的取值范围．

【题目】（本小题满分为14分）已知定义域为R的函数是奇函数．

（1）求a，b的值；

（2）若对任意的t∈R，不等式f（t2－2t）＋f（2t2－k）<0恒成立，求k的取值范围．

【题目】已知关于的二次函数.

（1）设集合和，分别从集合和中随机取一个数作为和，求函数在区间上是增函数的概率；

（2）设点是区域内的随机点，记事件“函数有两个零点，其中一个大于1，另一个小于1”为事件，求事件发生的概率.

【题目】已知点,椭圆的离心率为，是椭圆的右焦点，直线的斜率为，为坐标原点.

（I）求的方程；

（II）设过点的动直线与相交于两点，当的面积最大时，求的方程

【题目】设函数是定义在上的函数，并且满足下面三个条件：①对任意正数，都有；②当时， ；③.

（1）求， 的值；

（2）证明在上是减函数；

（3）如果不等式成立，求的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网