题目内容
已知函数
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数 ,
,
(1)求证:当 满足条件
满足条件 时,对于
时,对于 ,
, ;
;
(2)设 是两个实数,满足
是两个实数,满足 ,且
,且 ,若
,若 ,求函数
,求函数 在区间
在区间 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间 的长度定义为
的长度定义为 )
)

 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数 ,
,
(1)求证:当
 满足条件
满足条件 时,对于
时,对于 ,
, ;
;(2)设
 是两个实数,满足
是两个实数,满足 ,且
,且 ,若
,若 ,求函数
,求函数 在区间
在区间 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间 的长度定义为
的长度定义为 )
)(1)详见解析(2)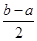
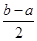
试题分析:(1)由分析可知
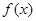 的解析式就是取
的解析式就是取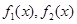 中较小的一个。所以
中较小的一个。所以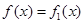 等价于
等价于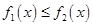 ,将此不等式转化成指数函数不等式
,将此不等式转化成指数函数不等式 ,根据指数的运算法则
,根据指数的运算法则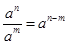 ,应将
,应将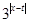 除过去用公式,再将不等式左边的2也化为以3为底的对数,依据的公式是
除过去用公式,再将不等式左边的2也化为以3为底的对数,依据的公式是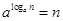 。再根据指数函数的单调性解同底的对数不等式。最后根据绝对值不等式的性质放缩不等式,即可求解。(2)根据(1)中所证已知
。再根据指数函数的单调性解同底的对数不等式。最后根据绝对值不等式的性质放缩不等式,即可求解。(2)根据(1)中所证已知 时,
时, ,图形关于
,图形关于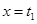 对称,且在
对称,且在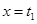 两侧单调性相反。若
两侧单调性相反。若 则
则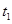 为
为 的中点。即可求得函数
的中点。即可求得函数 在区间
在区间 上的单调递增区间的长度。当
上的单调递增区间的长度。当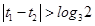 时,当
时,当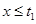 时
时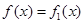 ,当
,当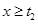 时
时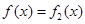 ,当
,当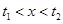 时解
时解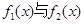 图象交点的横坐标,根据图像得
图象交点的横坐标,根据图像得 的解析式。再根据图像得增区间,再求增区间的长度。
的解析式。再根据图像得增区间,再求增区间的长度。试题解析:(1)由
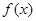 的定义可知,
的定义可知,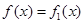 (对所有实数
(对所有实数 )等价于
)等价于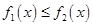 (对所有实数
(对所有实数 )这又等价于
)这又等价于 ,即
,即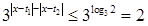 对所有实数
对所有实数 均成立. (*) 由于
均成立. (*) 由于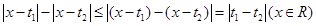 的最大值为
的最大值为 , 故(*)等价于
, 故(*)等价于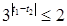 ,即
,即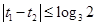 ,所以当
,所以当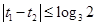 时,
时,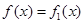
(2)分两种情形讨论
(i)当
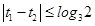 时,由(1)知
时,由(1)知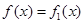 (对所有实数
(对所有实数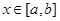 )
)则由
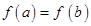 及
及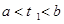 易知
易知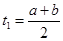 ,
, 再由
 的单调性可知,
的单调性可知,函数
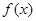 在区间
在区间 上的单调增区间的长度
上的单调增区间的长度为
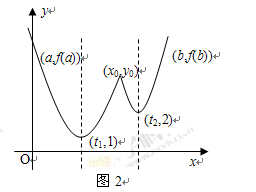
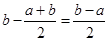 (参见示意图1)
(参见示意图1)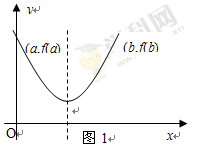
(ii)
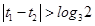 时,不妨设
时,不妨设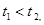 ,则
,则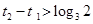 ,于是
,于是当
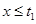 时,有
时,有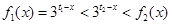 ,从而
,从而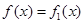 ;
;当
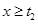 时,有
时,有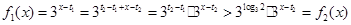
从而
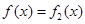 ;
;当
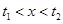 时,
时,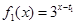 ,及
,及 ,由方程
,由方程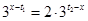
解得
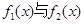 图象交点的横坐标为
图象交点的横坐标为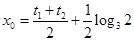 ⑴
⑴显然
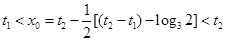 ,
,
这表明
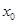 在
在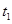 与
与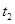 之间。由⑴易知
之间。由⑴易知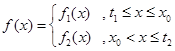
综上可知,在区间
 上,
上,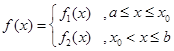 (参见示意图2)
(参见示意图2)故由函数
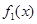 及
及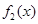 的单调性可知,
的单调性可知,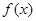 在区间
在区间 上的单调增区间的长度之和为
上的单调增区间的长度之和为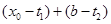 ,由于
,由于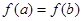 ,即
,即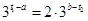 ,得
,得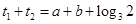 ⑵
⑵故由⑴、⑵得
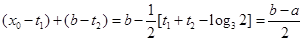
综合(i)(ii)可知,
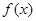 在区间
在区间 上的单调增区间的长度和为
上的单调增区间的长度和为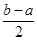 。
。
练习册系列答案
相关题目
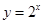 的图像向左平移一个单位,得到图像
的图像向左平移一个单位,得到图像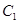 ,再将
,再将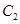 ,作出
,作出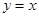 对称的图像
对称的图像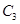 ,则
,则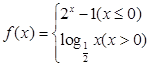 ,如果
,如果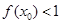 ,求
,求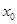 的取值范围.
的取值范围.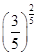 ,b=
,b=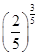 ,c=
,c=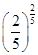 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )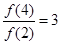 ,则
,则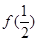 的值为 .
的值为 .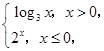 则f
则f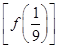 的值是( )
的值是( ) 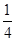
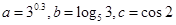 ,则( )
,则( )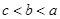
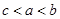
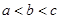
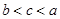
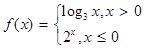 ,则
,则 .
.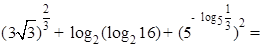 .
.